CONVERTING A QUADRATIC EQUATION FROM STANDARD FORM TO VERTEX FORM
To convert standard form to vertex form, we may follow the different ways.
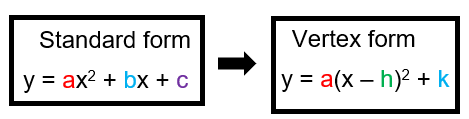
Completing the square method
From the standard form of the equation, y = ax2 + bx + c
Step 1 :
Factor the leading coefficient from x2 terms and x term.
Step 2 :
Write the coefficient of x as a multiple of 2.
Step 3 :
Comparing x2 terms and x term with the algebraic identity a2 + 2ab or a2 - 2ab, the missing term will be b2.
Step 4 :
So, add b2. In order to balance our work, we have to subtract b2.
Step 5 :
The first three terms will match with any one of the forms as a2 + 2ab + b2 or a2 - 2ab + b2, we can compress it as using the algebraic identities (a+b)2 or (a-b)2.
Step 6 :
After combining the like terms, we get the vertex form
y = a(x - h)2 + k
(or)
y = -a(x - h)2 + k
Using short cut
From the standard form of the equation, y = ax2 + bx + c
(i) Factor the leading coefficient from x2 term and x term.
(ii) Take half of the coefficient of x and write it as (x - a)2 or (x + a)2. Here a is half the coefficient of x.
Write each function in vertex form :
Problem 1 :
y = x2 - 6x + 3
Solution :
y = x2 - 6x + 3
The leading coefficient is 1. So, let us write the coefficient of x as multiple of 2.
y = x2 - 2x(3) + 3
Comparing the first two terms x2 - 2x(3), looks like a2 - 2ab. In order to complete the formula, we need b2. Then add b2, to balance our work, we need to write -b2.
y = x2 - 2x(3) + 32 - 32 + 3
Now combining a2 - 2ab + b2, we get (a - b)2.
y = (x - 3)2 - 32 + 3
y = (x - 3)2 - 9 + 3
y = (x - 3)2 - 6
Vertex of the parabola is (3, -6).
Problem 2 :
y = x2 + 2x + 7
Solution :
y = x2 + 2x + 7
The leading coefficient is 1. So, let us write the coefficient of x as multiple of 2.
y = x2 + 2x(1) + 7
y = x2 + 2x(1) + 12 - 12 + 7
y = (x + 1)2 - 1 + 7
y = (x + 1)2 + 6
Vertex of the parabola is (-1, 6).
Problem 3 :
y = x2 + 9x + 7
Solution :
y = x2 + 9x + 7
The leading coefficient is 1. So, let us write the coefficient of x as multiple of 2. Here the coefficient of x is 9, which is odd number. In order to write it as multiple of 2, we multiply and divide by 2.
So, the vertex of the parabola is (-9/2, -49/4).
Problem 4 :
y = -3x2 + 12x - 10
Solution :
y = -3x2 + 12x - 10
Factoring -3 from x2 term and x term, we get
y = -3[x2 - 4x] - 10
y = -3[x2 - 2 x (2) + 22 - 22] - 10
y = -3[(x - 2)2 - 4] - 10
y = -3(x - 2)2 + 12 - 10
y = -3(x - 2)2 + 2
The vertex of the parabola is (2, 2).
Problem 5 :
y = 3x2 + 10x
Solution :
y = 3x2 + 10x
Factoring -3 from x2 term and x term, we get
y = 3[x2 + (10/3)x]
y = 3[x2 + 2 ⋅ x ⋅ (5/6) + (5/6)2 - (5/6)2]
y = 3[(x + (5/6))2 - (5/6)2]
y = 3[(x + (5/6))2 - (25/36)]
y = 3(x + (5/6))2 - (25/12)
The vertex of the parabola is (-5/6, -25/12).
Problem 6 :
y = x2 - 12x + 36
Solution :
y = x2 - 12x + 36
y = x2 - 2 x (6) + 62 - 62 + 36
y = x2 - 2 x (6) + 62 - 36 + 36
y = (x - 6)2
So, the vertex of the parabola is (6, 0).
Problem 7 :
y = -4x2 - 24x - 15
Solution :
y = -4x2 - 24x - 15
y = -4[x2 + 6x] - 15
y = -4[x2 + 2 x (3) + 32 - 32] - 15
y = -4[(x + 3)2 - 9] - 15
y = -4(x + 3)2 + 36 - 15
y = -4(x + 3)2 + 21
So, the vertex of the parabola is (-3, 21).
Problem 8 :
y = -x2 - 4x - 1
Solution :
y = -x2 - 4x - 1
y = -[x2 + 4x] - 1
y = -[x2 + 2x(2) + 22 - 22] - 1
y = -[(x + 2)2 - 4] - 1
y = -(x + 2)2 + 4 - 1
y = -(x + 2)2 + 3
So, the vertex of the parabola is (-2, 3).
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling