CONVERTING A CIRCLE FROM ONE SHAPE TO ANOTHER

Problem 1 :

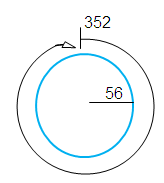
A wire can be bent in the form of a circle of radius 56 cm. If it is bent in the form of a square, then its area will be

(a)  3520 cm²  (b)  6400 cm²  (c)  7744 cm²   (d)  8800cm²

Solution :

Radius  = 56 cm

Circumference of circle = 2πr

= 2 × 22/7 × 56

Circumference of circle = 352 cm

Perimeter of a square =  4a

352 = 4a

a = 352/4

a = 88 cm

Area of square = a²

= 88 cm × 88 cm

Area of square = 7744 cm²

So, option c) is correct.

Problem 2 :

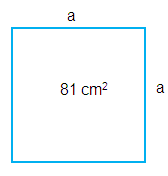
If a wire is bent into the shape of a square, then the area of the square is 81 cm². When wire is bent into a semi-circular shape, then the area of the semi-circle will be

(a)  22 cm²  (b)  44 cm²   (c)  77 cm²   (d)  154 cm²

Solution :

Area of square = 81 cm²

Area of square = a²

81 = a²

a = 9 cm

Perimeter of square = 4a

= 4(9)

 = 36 cm

Perimeter of semi-circular = πr + 2r

36 = r(π + 2)

36 = r(22/7 + 2)

36 = r(36/7)

r = 7 cm

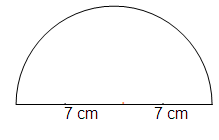
area of the semi circular = 1/2(πr²)

= 1/2(22/7 × 72)

= 1/2(22/7 × 49)

= 77 cm²

So, option c) is correct.

Problem 3 :

The circumference of a circle is 100cm. The side of a square inscribed inthe circle is

(a)  50√2 cm   (b)  100/π cm   (c)  50√2/π cm  (d)  100√2/π cm

Solution :

circumference of a circle = 100cm.

2πr = 100

r = 100/2π

r = 50/π cm

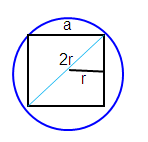
Diagonal of square = Diameter of circle

√2 a = 2r

√2 a = 2(50/π)

√2 a = 100/π

a = 100/π × 1/√2

a = 100/π × (1/√2 × √2/√2)

a = 100/π × √2/2

a = 50√2/π

So, option c) is correct.

Problem 4 :

If an arc of a circle forms 90^º at the centre of the circle, then the ratio of its length to the circumference of the circle is 

(a)  1 : 4    (b)   3 : 4   (c)  1 : 3   (d)  2 : 3

Solution :

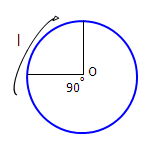
θ = 90^º

Length of the arc = θ/360^º × 2πr

= 90^º/360^º × 2πr

= 1/4 × 2πr

Circumference of a circle = 2πr

Ratio of its length to the circumference of the circle

= Length of the arc/circumference of a circle

= 1/4 × 2πr/2πr

= 1/4

So, ratio of its length to the circumference of the circle is 1 : 4.

So, option a) is correct.

Problem 5 :

The area of a circle is 220cm². The area of square inscribed in it is

(a)  49 cm²  (b)  70 cm²  (c)  140 cm²  (d)  150 cm²

Solution :

area of a circle = 220cm²

area of a circle = πr²

220 = πr²

220 = 22/7 × r²

220 × 7/22 = r²

70 = r²

r = √70

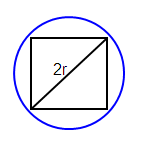
Diagonal of square = Diameter of circle

√2 a = 2r

√2 a = 2(√70)

a = 2(√70/√2)

a = 2(√35)

area of square = a²

= 2²(√35)²

= 140

So, option c) is correct.

Problem 6 :

The area of the circle that can be inscribed in a square of side 6 cm is

(a)  36 π cm²   (b)   18 π cm²  (c)  12 π cm²   (d)   9 π cm²

Solution :

Sides of a square = 6 cm

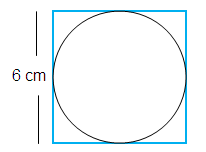
Radius of the circle = 6/2

r = 3

Area of the circle = πr²

= π(3)²

= 9π

So, option d) is correct.

Problem 7 :

The area of the square that can be inscribed in a circle of radius 8 cm is

(a)  256 cm²   (b)   128 cm²  (c)  64√2 cm²   (d)   64 cm²

Solution :

radius of circle = 8 cm

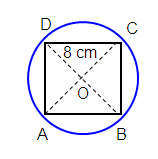
diameter of the circle = AC

= 2 × OC

= 2 × 8

= 16 cm

Let 'a' be the side of square.

Using Pythagorean theorem.

AC² = AB² + BC²

(16)² = a² + a²

256 = 2a²

a² = 256/2

a² = 128

So, area of square is 128 cm².