CONVERT FROM GENERAL FORM TO STANDARD FORM OF A CIRCLE
Write each of the following in standard form. Identify the center of the circle as well as the length of the radius, the graph the circle if possible.
Problem 1 :
x2 + y2 + 10x - 4y + 13 = 0
Solution :
x2 + y2 + 10x - 4y + 13 = 0
Write x - terms and y - terms together.
x2 + 10x + y2 - 4y + 13 = 0
Completing the square.
x2 + 10x + 52 - 52 + y2 - 4y + 22 - 22 + 13 = 0
(x + 5)2 - 52 + (y - 2)2 - 22 + 13 = 0
(x + 5)2 - 25 + (y - 2)2 - 4 + 13 = 0
(x + 5)2 + (y - 2)2 - 16 = 0
Add 16 to each side.
(x + 5)2 + (y - 2)2 = 16
(x + 5)2 + (y - 2)2 = 42
The above equation of the circle is in standard form.
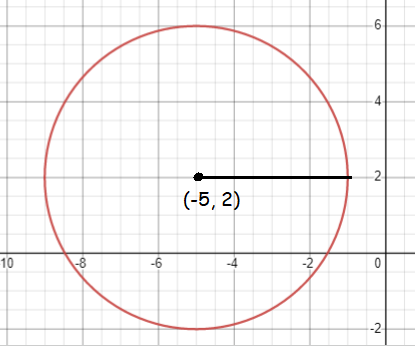
Center (h, k) = (-5, 2)
Radius = 4
Problem 2 :
x2 + y2 + 6y - 16 = 0
Solution :
x2 + y2 + 6y - 16 = 0
Write x - terms and y - terms together.
x2 + y2 + 6y - 16 = 0
Completing the square.
x2 + y2 + 6y + 32 - 32 - 16 = 0
x2 + (y + 3)2 - 32 - 16 = 0
x2 + (y + 3)2 - 9 - 16 = 0
x2 + (y + 3)2 - 25 = 0
Add 25 on each sides.
x2 + (y + 3)2 = 25
x2 + (y + 3)2 = 52
The above equation of the circle is in standard form.
Center (h, k) = (0, -3)
Radius = 5
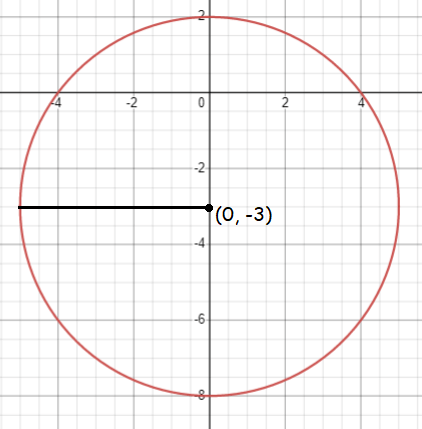
Problem 3 :
x2 + y2 - 4x - 8y + 11 = 0
Solution :
x2 + y2 - 4x - 8y + 11 = 0
Write x - terms and y - terms together.
x2 - 4x + y2 - 8y + 11 = 0
Completing the square.
x2 - 4x + 22 - 22 + y2 - 8y + 42 - 42 + 11 = 0
(x - 2)2 - 22 + (y - 4)2 - 42 + 11 = 0
(x - 2)2 - 4 + (y - 4)2 - 16 + 11 = 0
(x - 2)2 + (y - 4)2 - 9 = 0
Add 9 to each side.
(x - 2)2 + (y - 4)2 = 9
(x - 2)2 + (y - 4)2 = 32
The above equation of the circle is in standard form.
Center (h, k) = (2, 4)
Radius = 3
Problem 4 :
x2 + y2 + 6x - 8y + 29 = 0
Solution :
x2 + y2 + 6x - 8y + 29 = 0
Write x - terms and y - terms together.
x2 + 6x + y2 - 8y + 29 = 0
Completing the square.
x2 + 6x + 32 - 32 + y2 - 8y + 42 - 42 + 29 = 0
(x + 3)2 - 32 + (y - 4)2 - 42 + 29 = 0
(x + 3)2 - 9 + (y - 4)2 - 16 + 29 = 0
(x + 3)2 + (y - 4)2 + 4 = 0
Subtract 4 on each sides.
(x + 3)2 + (y - 4)2 = -4
There is no circle.
Problem 5 :
x2 + y2 - 8x - 20 = 0
Solution :
x2 + y2 - 8x - 20 = 0
Write x - terms and y - terms together.
x2 - 8x + y2 - 20 = 0
Completing the square.
x2 - 8x + 42 - 42 + y2 - 20 = 0
(x - 4)2 - 42 + y2 - 20 = 0
(x - 4)2 - 16 + y2 - 20 = 0
(x - 4)2 + y2 - 36 = 0
Add 36 to each sides.
(x - 4)2 + y2 = 36
(x - 4)2 + y2 = 6
The above equation of the circle is in standard form.
Center (h, k) = (4, 0)
Radius = 6
Problem 6 :
2x2 + 2y2 + 4x - 12y + 2 = 0
Solution :
2x2 + 2y2 + 4x - 12y + 2 = 0
2(x2 + y2 + 2x - 6y + 1) = 0
Dividing 2 on each sides.
x2 + y2 + 2x - 6y + 1 = 0
Write x - terms and y - terms together.
x2 + 2x + y2 - 6y + 1 = 0
Completing the square.
x2 + 2x + 12 - 12 + y2 - 6y + 32 - 32 + 1 = 0
(x + 1)2 - 12 + (y - 3)2 - 32 + 1 = 0
(x + 1)2 - 1 + (y - 3)2 - 9 + 1 = 0
(x + 1)2 + (y - 3)2 - 9 = 0
Add 9 to each side.
(x + 1)2 + (y - 3)2 = 9
(x + 1)2 + (y - 3)2 = 32
The above equation of the circle is in standard form.
Center (h, k) = (-1, 3)
Radius = 3
Problem 7 :
3x2 + 3y2 + 36x + 30y + 171 = 0
Solution :
3x2 + 3y2 + 36x + 30y + 171 = 0
3(x2 + y2 + 12x + 10y + 57) = 0
Dividing 3 on each sides.
x2 + y2 + 12x + 10y + 57 = 0
Write x - terms and y - terms together.
x2 + 12x + y2 + 10y + 57 = 0
Completing the square.
x2 + 12x + 62 - 62 + y2 + 10y + 52 - 52 + 57 = 0
(x + 6)2 - 62 + (y + 5)2 - 52 + 57 = 0
(x + 6)2 - 36 + (y + 5)2 - 25 + 57 = 0
(x + 6)2 + (y + 5)2 - 4 = 0
Add 4 to each sides.
(x + 6)2 + (y + 5)2 = 4
(x + 6)2 + (y + 5)2 = 22
The above equation of the circle is in standard form.
Center (h, k) = (-6, -5)
Radius = 2
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling