CONTINUITY AND DIFFERENTIABILITY PROBLEMS FOR AP CALCULUS AB

Problem 1 :

Let f be the function such that 

I. f is continuous at x = 4.

II f is differentiable at x = 4.

III. The derivative of f' is continuous at x = 4.

A) I only   B)  II only    C) I and II only   D)  I, II and III only

Solution :

The given should be considered as derivative of f(x) at x = 4, since it exists, it is continuous and differentiable at x = 4.

From here we cannot decide anything about the derivative of f'(x), so the answer is I and II only.

Problem 2 :

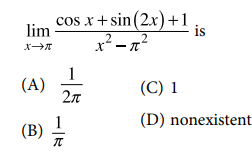
Solution :

Using l'hopital rule,

Problem 3 :

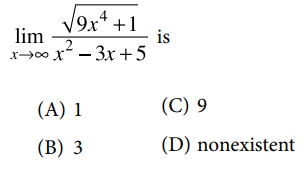
Solution :

Problem 4 :

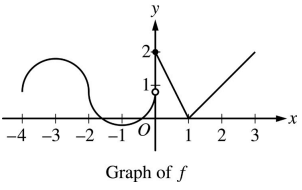
The graph of the piecewise defined function f is shown in the figure above. The graph has a vertical tangent line at x = -2 and horizontal lines x = -3 and x = -1 What are all values of x, -4 < x < 3 at which f is continuous but not differentiable ?

A) x = 1     B)  x = -2 and x = 0     C)  x = -2 and x = 1

D)  x = 0 and x = 1

Solution :

Option A:

At x = 1, the function is continuous.

Option B:

At x = -2, the function is continuous but at x = 0, the function is not continuous.

Option C :

At vertical tangent line, at the points where it is discontinuous and at sharp edges or cusp, the function is not differentiable.

At x = -2, we draw the vertical tangent line. So, at x = -2 the function is not differentiable. At x - 1, we have a sharp edge. 

At these two points the function is not differentiable. So, option C is correct.

Problem 5 :

A)  I only      B)  II only     C)   I and II only     D)  I, II and III

Solution :

I

II

III

So, option B II is correct.

Problem 6 :

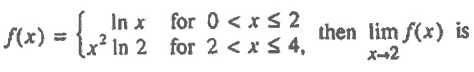
A) ln 2     B)  ln 8    C)  ln 16     D)  4    E) Non existent

Solution :

lim _x->2- f(x) = lim _x->2- ln x

= ln (2) --------(1)

lim _x->2+ f(x) = lim _x->2+ x²ln x

= 4ln (2) --------(2)

(1) ≠ (2)

So, the limit does not exists.

Problem 7 :

A particle moves along the x-axis so it s position at time t is given by

x(t) = t² - 6t + 5

For what value of t is the velocity of the particle zero ?

Solution :

x(t) = t² - 6t + 5

x'(t) = 2t - 6

v(t) = 2t - 6

Velocity = 0

2t - 6 = 0

t = 3

Problem 8 :

Let be the function defined by

Which of the following statements is true?

A) has a discontinuity due to a vertical asymptote at x = 0 and at x = 4 .

B)  has a removable discontinuity at x = 0 and a jump discontinuity at x = 4

C)  has a removable discontinuity at x = 0 and a discontinuity due to a vertical asymptote at x = 4

D)  is continuous at x = 0, and has a discontinuity due to a vertical asymptote at x = 4.

Solution :

The common factor is x, then it has removable discontinuity at x = 0 and at x = 4, we have vertical asymptote.

So, the answer is C.