CONIC SECTION PROBLEMS ON ELLIPSE AND HYPERBOLA

Problem 1 :

The eccentricity of the hyperbola whose latus rectum is 8 and conjugate axis is equal to half of the distance between the foci is 

a)  4/3      b) 4/√3      c)  2/√3        d)  3/2

Solution :

Length of latus rectum = 2b²/a

2b²/a = 8

b²= 4a ------(1)

Length of conjugate axis = half the distance between foci

2b = ae

b = ae/2

Applying the value of b in (1), we get

(ae/2)² = 4a

a²e² = 16a

e² = 16/a

b² = a² (e² - 1)

4a = a² (16/a - 1)

4a = 16a - a²

a² -16a + 4a = 0

a² -12a = 0

a(a - 12) = 0

a = 0 and a = 12

e² = 16/a

e² = 16/12

e = √(16/12)

e = √(4/3)

e = 2/√3

So, the eccentricity is 2/√3.

Problem 2 :

If P(x, y) be any point on 16x² + 25y² = 400 and foci F1(-3, 0) then PF1 + PF2 is 

a)  8     b)  6    c)  10     d)  12

Solution :

The given is equation of ellipse and it is symmetric about x-axis.

a = 25, b = 4

F1 P + F2 P = 2a

2a = 2(5)

= 10

Problem 3 :

The area of quadrilateral formed with foci of the hyperbolas 

a)  4(a² + b²)      b) 2(a² + b²)

c) (a² + b²)           d) 1/2(a² + b²)

Solution :

The first hyperbola is symmetric about x-axis. Its foci are (ae, 0) and (-ae, 0).

The above hyperbola is symmetric about y-axis. Its foci are (0, ae) and (0, -ae).

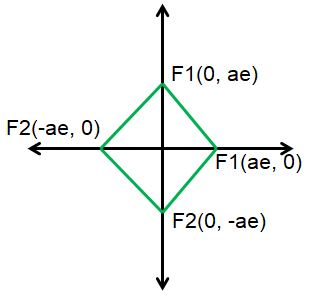
It is a rhombus.

Area of rhombus = (1/2) x d1 x d2

= (1/2) x (2ae) x (2ae)

= 2a² e²

b² = a² (e² - 1)

b² = a² e² - a²

a² + b² = a² e² 

Multiplying by 2 on both sides, we get

2(a² + b²) = 2a² e² 

So, the required area is 2(a² + b²).

Problem 4 :

If the normals of the parabola y² = 4x drawn at the end points of its latus rectum are tangents to the circle (x - 3)² + (y + 2)² = r², then the value of r² is 

a)  2      b)  3      c)   1       d)      4

Solution :

y² = 4x

y² = 4ax

4a = 4

a = 1

Endpoints of latus rectum are :

x = 1

y² = 4(1)

y = √4

y = ±2

(1, 2) and (1, -2)

(x - 3)² + (y + 2)² = r²

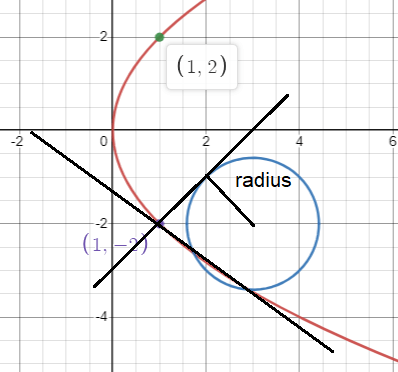
Equation of normal drawn at the point (1, -2).

Equation of tangent for the parabola y² = 4x

yy₁ = 4 (x + x₁)/2

yy₁ = 2 (x + x₁)

y(-2) = 2(x + 1)

-2y = 2x + 2

y = -x - 1, slope of tangent = -1

slope of normal = 1

Equation of normal at the point (1, -2)

y + 2 = 1(x - 1)

y = x - 1 - 2

x - y - 3 = 0

Perpendicular distance between x - y - 3 at the center (3, -2)

distance = |3 - (-2) - 3| / √1²+1²

= |2| / √2

r = 2/√2

r² = (2/√2)²

r² = (4/2)

r² = 2

Problem 5 :

If x+y = k is a normal to the parabola y² = 12x, then the value of k is 

a)  3    b)  -1    c)  1      d)  9

Solution :

Equation of parabola y² = 12x

4a = 12

a = 3

Equation of normal :

y + xt = at³ + 2at

y + xt = 3t³ + 6t

x + y = k

Using cross product rule to solve for t,

1/1 = 1/t = (3t³ + 6t)/k

So, the answer is option d.

Problem 6 :

The ellipse E1 :

is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribing the rectangle R. The eccentricity of the ellipse is 

a) √2/2    b)  √3/2    c)  1/2      d)  3/4

Solution :

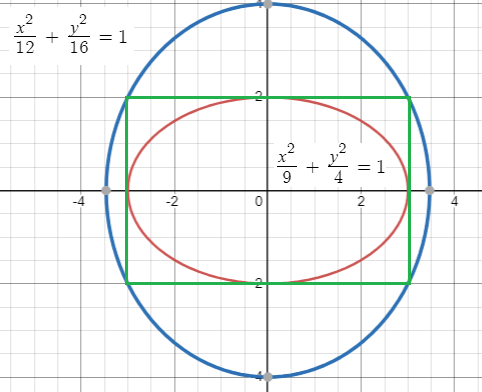
The ellipse symmetric about y-axis.

The value of a² will be greater than b²

a² = 16

By observing the above picture, the ellipse is passing through the point (-3, 2).