CONGRUENT CHORDS AND ARCS
In the same circle, or in congruent circles,
two minor arcs are congruent if and only if their corresponding chords are
congruent.
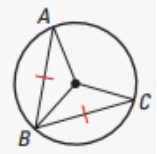
AB ≈ BC if and only if AB ≈ BC
Problem 1:
Find the measure of AB.
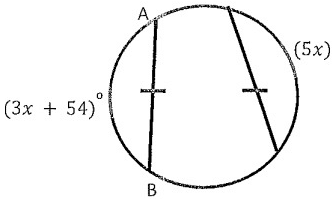
Solution :
3x + 54˚ = 5x
5x - 3x = 54˚
2x = 54
x = 27˚
AB = 3(27) + 54
= 81 + 54
AB = 135˚
Problem 2 :
In circle B, CB ≈ BD. Find x if AE = x² and FG = 3x + 4.
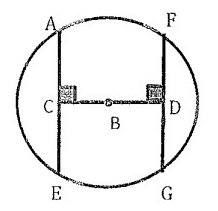
Solution :
In the above diagram, the two chords AE and FG are congruent.
AE = FG
x² = 3x + 4
x² - 3x - 4 = 0
(x + 1) (x - 4) = 0
x = -1 or x = 4
We can use only positive value for x.
So,
x = 4
Problem 3 :
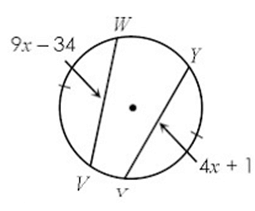
Solution :
In the above diagram, the two chords VW and XY are congruent.
WV = XY
9x - 34 = 4x + 1
9x - 4x = 1 + 34
5x = 35
x = 7
Problem 4 :
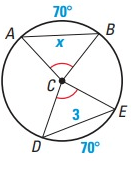
Solution :
Equal chords of a circle subtend equal angles at the center.
∠ACB = ∠DCE
AB = DE
x = 3
Problem 5 :
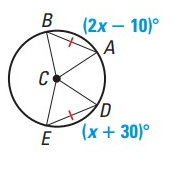
Solution :
AB = DE
2x - 10˚ = x + 30˚
2x - x = 30 + 10
x = 40˚
Problem 6 :
Use the diagram below.
a. Explain why AD ≈ BE.
b. Find the value of x.
c. Find m arc AD and m arc BE.
d. Find m arc BD.
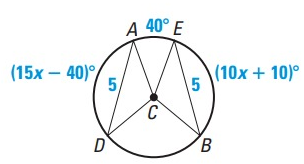
Solution :
a.
In the diagram above, the two chords AD and BE are congruent.
AD ≈ BE
b.
15x - 40 = 10x + 10
15x - 10x = 10 + 40
5x = 50
x = 10
c.
m arc AD = 15x - 40˚
= 15(10) - 40
= 150 - 40
m arc AD = 110˚
m arc BE = 10x + 10˚
= 10(10) + 10
= 100 + 10
m arc AD = 110˚
d.
m arc BD = 360˚ - (110 + 110 + 40)˚
= 360˚ - 260˚
m arc BD = 100˚
Problem 7:
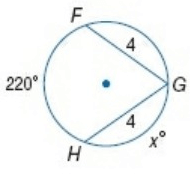
Solution :
Given, FG = HG = 4
m arc HG = m arc FG =
x + x + 220 = 360
2x = 360 - 220
x = 140/2
x = 7
Problem 8 :
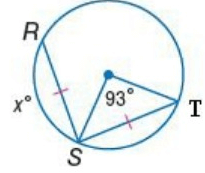
Solution :
RS = ST
So,
x = 93˚
Problem 9 :
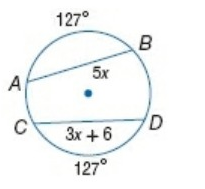
Solution :
In the diagram above, the two chords AB and CD are congruent.
AB = CD
5x = 3x + 6
5x - 3x = 6
2x = 6
x = 3
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling