COMPOSITION OF TWO FUNCTIONS

Problem 1 :

Given f(x) = -9x + 3 and g(x) = x⁴, find (f ∘ g)(x)

Solution:

(f ∘ g)(x) = f[g(x)]

= f[x⁴]

= -9(x⁴) + 3

= -9x⁴ + 3

Problem 2 :

Given f(x) = 2x - 5 and g(x) = x + 2, find (f ∘ g)(x)

Solution:

(f ∘ g)(x) = f[g(x)]

= f[x + 2]

= 2(x + 2) - 5

= 2x + 4 - 5

= 2x - 1

Problem 3 :

Given f(x) = x² + 7 and g(x) = x - 3, find (f ∘ g)(x)

Solution:

(f ∘ g)(x) = f[g(x)]

= f[x - 3]

= (x - 3)² + 7

= x² - 2(x)(3) + 3² + 7

= x² - 6x + 16

Problem 4 :

Given f(x) = 4x + 3 and g(x) = x², find (g ∘ f)(x)

Solution:

(g ∘ f)(x) = g[f(x)]

= g[4x + 3]

= (4x + 3)²

= (4x)² + 2(4x)(3) + 3²

= 16x² + 24x + 9

Problem 5 :

Given f(x) = x - 1 and g(x) = x² + 2x - 8, find (g ∘ f)(x)

Solution:

(g ∘ f)(x) = g[f(x)]

= g[x - 1]

= (x - 1)² + 2(x - 1) - 8

= x² - 2x + 1 + 2x - 2 - 8

= x² - 9

Problem 6 :

If f(x) = -2x + 1 and g(x) = √x² - 5, find (g ∘ f)(2).

Solution:

(g ∘ f)(x) = g[f(x)]

= g[-2x + 1]

= g[-2(2) + 1]

= g(-3)

=  √(-3)² - 5

=  √(9 - 5)

= √4

= 2

Problem 7 :

If f(x) = -4x + 2 and g(x) = √(x - 8), find (f ∘ g)(12).

Solution:

(f ∘ g)(x) = f[g(x)]

= f[√(x - 8)]

= f[√(12 - 8)]

= f[√4]

= f(2)

= -4(2) + 2

= -8 + 2

= -6

Problem 8 :

If f(x) = -3x + 4 and g(x) = x², find (g ∘ f)(-2).

Solution:

(g ∘ f)(x) = g[f(x)]

= g[-3x + 4]

= g[-3(-2) + 4]

= g[10]

= (10)²

= 100

Problem 9 :

If possible, use the given representations of functions ƒ and g to evaluate

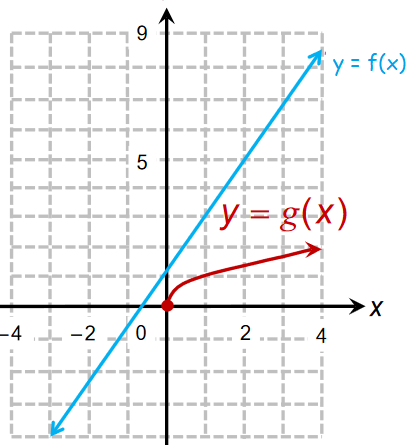
1)  (f + g) (4)       2)  (f - g) (-2)      3)  fg (1)    4) (f/g) (0)

Solution :

1)  (f + g) (4) :

= f(4) + g(4)

= 8.5 + 2

= 10.5

2)  (f - g) (-2) :

= f(-2) - g(-2)

= -2 - undefined

= -2

3)  fg (1) :

= f(1) g(1)

= 3 (1)

= 3

4) (f/g) (0) :

= f(0) / g(0)

= 1/0

= undefined

Problem 10 :

If possible, use the given representations of functions ƒ and g to evaluate

1)  (f + g)(4)       2)  (f - g)(-2)     3)  (fg)(1)    4)  (f/g)(0)

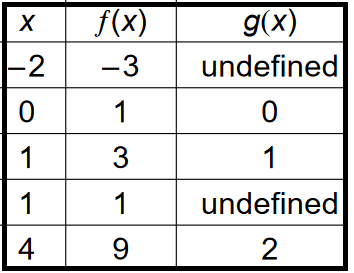
Solution :

1)  (f + g)(4)

= f(4) + g(4)

= 9 + 2

(f + g)(4) = 11

2)  (f - g)(-2)

= f(-2) - g(-2)

= -3 - undefined

(f - g)(-2) = -3

3)  (fg)(1)

= f(1) x g(1)

= 3 x 1

(fg)(1) = 3

4)  (f/g)(0)

= f(0) / g(0)

= 1 x 0

(f/g)(0) = 0

Problem 11 :

The radius r, in inches, of a spherical balloon is related to the volume, V, by

Air is pumped into the balloon, so the volume after t seconds is given by V(t) = 10 + 20t.

a. Find the composite function r(V(t))

b. Find the radius after 20 seconds

Solution :

a)

b)