COMPARING TWO DISTRIBUTION USING DOT PLOTS

Problem 1 :

Martha conducted a random survey during lunch. She asked 20 students and 20 teachers how many siblings they have. The survey data are represented in the dot plots below. Based on the data in the dot plots, fill in the blanks to create a true statement.

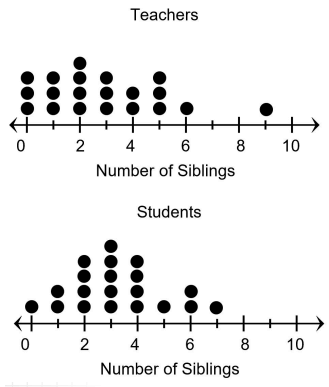
1) The range of the data for the survey results for teachers is _________ than the range of the data for the survey results for the students.

2) The mode of the data for the survey results for teachers is _________ than the mode of the data for the survey results for the students.

3) The data for the survey for _________ is more symmetrical than the data for the survey for _________.

4) The median of the data for the survey results for teachers is _________ than the median of the data for the survey results for the students.

5) The greatest number of siblings for teachers is _________ than the greatest number of siblings for students.

Solution :

Range of data for teachers = 9 - 0 ==> 9

Range of data for students = 7 - 0 ==> 7

1) The range of the data for the survey results for teachers is greater than the range of the data for the survey results for the students.

Mode for teachers = 2, mode for students = 3

2) The mode of the data for the survey results for teachers is lesser than the mode of the data for the survey results for the students.

3) The data for the survey for students is more symmetrical than the data for the survey for teachers

Data for teachers :

0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 9

Median for teachers = 20/2 ^th element 

= 10^th element

Median = 2

Data for students :

0, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 6, 6, 7

 = 10^th element

Median = 3

Greatest number of siblings for teacher = 2

Greatest number of siblings for students = 3

5) The greatest number of siblings for teachers is lesser than the greatest number of siblings for students.

Problem 2 :

Use the following information for questions. Determine if each statement is true or false.

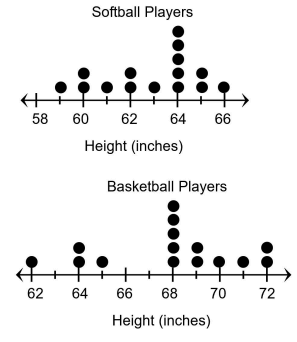
1) The range of the data for the heights of softball players is less than the range of the data for the heights of basketball players.

2) The median of the data for the heights of softball players is greater than the median of the data for the heights of basketball players.

Solution :

Range for softball players = 66 - 59 ==> 7

Range for basket ball players = 72 - 62 ==> 10

Softball players :

59, 60, 60, 61, 62, 62, 63, 64, 64, 64, 64, 64, 65, 65, 66

Median = (15 + 1)/2

= 8^th

Median = 64

Basket ball players :

62, 64, 64, 65, 68, 68, 68, 68, 68, 69, 69,70, 71, 72, 72

= 8th element

Median = 68

1) True    2) False

Problem 3 :

The dot plots below represent two sets of data. 

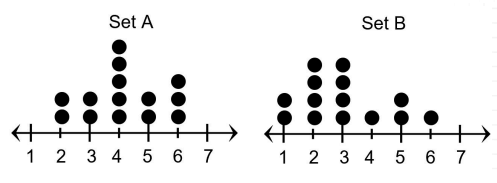
Here are three statements about the data.

I. The mode of the data in Set A is equal to the mode of the data in Set B.

II. The range of the data in Set A is less than the range of the data in Set B.

III. The median of the data in Set A is greater than the median of the data in Set B.

Which of these three statements appear to be true?

F I only          G I and II            H II and III         J III only

Solution :

Mode of set A is 4, mode of set B is 2 and 3.

Range of set A = 6 - 2 ==> 4

Range of set B = 6 - 1 ==> 5

Average of 7th and 8th data is 4. So, median of set A is 4.

Average of 7th and 8th data is 3. So, median of set A is 3.

III only true.