COMPARING LINEAR FUNCTIONS

Examine each set of functions and determine which has the greater rate of change, if either. Explain your reasoning.

Problem 1 :

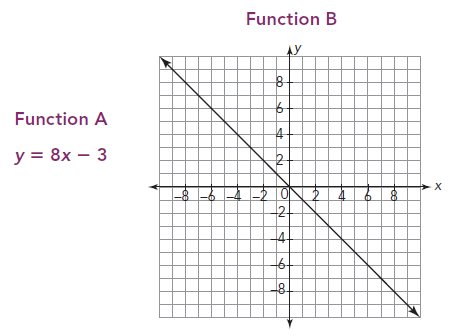
Solution :

From function A :

y = 8x - 3

Comparing the given equation with slope intercept form

y = mx + b

m = 8

From function B :

Taking two points on the graph, (0, 0) and (2, 2)

(x₁, y₁) ==> (0, 0) and (x₂, y₂) ==> (2, 2)

Change in y = (2 - 0) ==> 2

Change in x = (2 - 0) ==> 2

Slope = Change in y / change in x ==> 2/2 ==> 1

Function A is having greater rate of change.

Problem 2 :

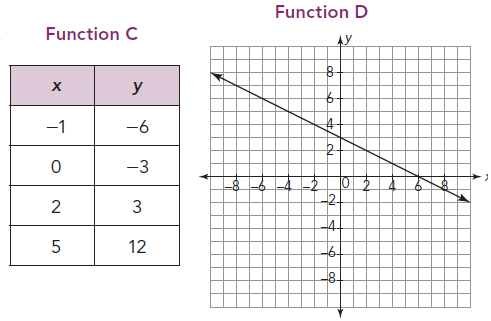
Solution :

Rate of change from function C :

Taking two points from the table, (-1, -6) and (0, -3).

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

m = (3 + 6) / (0 + 1)

m = 9/1

m = 9

Rate of change from function D :

Taking two points from the table, (0, 3) and (6, 0).

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

m = (0 - 3) / (6 - 0)

m = -3/6

m = -1/2

Function C is having greater rate of change.

Problem 3 :

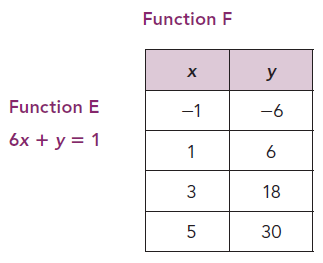
Solution : 

Rate of change from equation E :

6x + y = 1

Converting the given equation into slope intercept form, we get

y = -6x + 1

Slope (m) = -6

Rate of change from equation F :

Two points from the graph (-1, -6) and (1, 6).

Change in y = (6 +6) ==> 12

Change in x = (1 + 1)  ==>  2

Slope (m) = Change in y / change in x

Slope (m) = 12/2

m = 6

Equation F is having grater rate of change.

Problem 4 :

Alicia, Cherie, and John had been studying rates of change and were discussing the best way to determine which linear function has the greater rate of change.

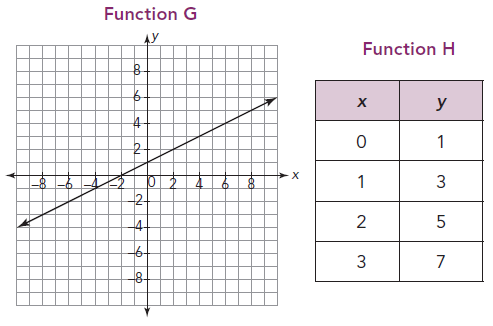
Solution :

Rate of change from G :

Considering two points on the line (0, 1) and (4, 3).

Change in y = (3 - 1) ==> 2

Change in x = (4 - 0) ==> 4

Slope = 2/4 ==> 1/2

Rate of change from H :

Two points from the table are (0, 1) and (1, 3).

m = (3 - 1) / (1 - 0)

m = 2/1

m = 2

So, function H is having greater rate of change.

Problem 5 :

Match each description of the situation with its corresponding graph. Explain your reasoning.

a. A person gives $20 per week to a friend to repay a $200 loan.

b. An employee receives $12.50 per hour plus $2 for each unit produced per hour.

c. A sales representative receives $30 per day for food plus $0.565 for each mile driven.

d. A computer that was purchased for $750 depreciates $100 per year.

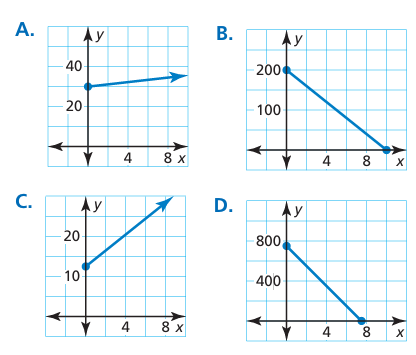
Solution :

Graph A :

• y-intercept = 30
• Slope = it is increasing line, so it must have positive slope.

Correct answer :

c) A sales representative receives $30 per day for food plus $0.565 for each mile driven.

Graph B :

• y-intercept = 200
• To find slope, we choose two points. (0, 200) and (9, 0)
• Slope = (0 - 200) / (9 - 0)
• -200/9 = 22.2 (approximatley)

Correct answer :

a) A person gives $20 per week to a friend to repay a $200 loan.

Graph C :

• y-intercept = 13 (approximately)
• To find slope, we choose two points. (0, 13) and (4, 20)
• Slope = (20 - 13) / (4 - 0)
• 7/4 = 1.75 (approximatley)

Correct answer :

b) An employee receives $12.50 per hour plus $2 for each unit produced per hour.

Graph D :

• y-intercept = 750(approximately)
• To find slope, we choose two points. (0, 13) and (4, 20)
• Slope = (20 - 13) / (4 - 0)
• 7/4 = 1.75 (approximatley)

Correct answer :

d) A computer that was purchased for $750 depreciates $100 per year.

Problem 6 :

The function C(x) = 17.5x − 10 represents the cost (in dollars) of buying x tickets to the orchestra with a $10 coupon.

a. How much does it cost to buy five tickets?

b. How many tickets can you buy with $130?

Solution :

C(x) = 17.5x − 10

Here x is the number of tickets.

a)  Number of tickets = 5

C(5) = 17.5(5) - 10

= 87.5 - 10

= 77.5

b) C(x) = 130

130 = 17.5x − 10

130 + 10 = 17.5x

140 = 17.5x

x = 140/17.5

x = 8

Problem 7 :

Account A earns simple interest. Account B earns compound interest. The table shows the balances for 5 years. Graph the data and compare the graphs.

Solution :

The balance of Account A has a constant rate of change of $10. So, the function representing the balance of Account A is linear.

The balance of Account B increases by different amounts each year. Because the rate of change is not constant, the function representing the balance of Account B is nonlinear.