COMPARING AVERAGE RATE OF CHANGE FOR SQUARE ROOT FUNCTIONS

Problem 1 :

The velocity v (in meters per second) of an object in motion is given by

v(E ) = √(2E/m)

where E is the kinetic energy of the object (in joules) and m is the mass of the object (in kilograms). The mass of Object A is 4 kilograms.

The graph shows the velocity of Object B. Compare the velocities of the objects by finding and interpreting the average rates of change over the interval E = 0 to E = 6.

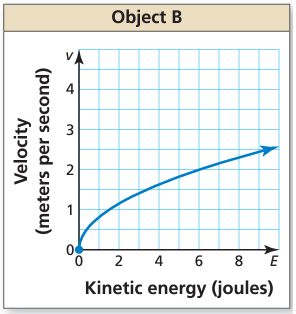
Solution :

Average rate of change from the equation :

From the velocity function, m = 4

v(E) = √(2E/m) ==> v(E) = √(2E/4) ==> v(E) = √(E/2)

Average rate of change = [v(6) - v(0)] / (6 - 0)

= (1.732 - 0) / (6 - 0)

= 1.732 / 6

= 0.288 m/sec

Average rate of change from the graph :

The two points traced from the curve over the given interval x = 0 and x = 6 are (0, 0) and (6, 2)

= (y₂ - y₁) / (x₂ - x₁)

= (2 - 0) / (6 - 0)

= 2/6

= 1/3

= 0.333 m/sec

The velocity of object A is lesser than velocity of object B.

Problem 2 :

The model S(d) = √30 df represents the speed S (in miles per hour) of a van before it skids to a stop, where f is the drag factor of the road surface and d is the length (in feet) of the skid marks. The drag factor of Road Surface A is 0.75.

The graph shows the speed of the van on Road Surface B. Compare the speeds by finding and interpreting their average rates of change over the interval d = 0 to d = 15.

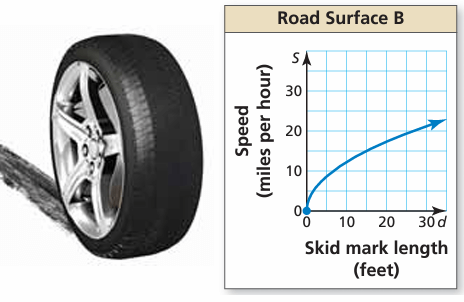
Solution :

S(d) = √30 df

Here f = 0.75

S(d) = √30 d(0.75)

S(d) = √22.5 d

Average rate of change over the interval :

d = 0 to d = 15

Average rate of change = (18.37 - 0) / (15 - 0)

= 18.37 / 15

= 1.22

Average rate of change from graph :

(0, 0) and (15, 15)

Average rate of change = (15 - 0) / (15 - 0)

= 15/15

= 1

Average rate of change of graph B is smaller.

Problem 3 :

The nozzle pressure of a fire hose allows firefighters to control the amount of water they spray on a fire. The flow rate f (in gallons per minute) can be modeled by the function

f = 120√p

where p is the nozzle pressure (in pounds per square inch).

a. Use a graphing calculator to graph the function. At what pressure does the flow rate exceed 300 gallons per minute?

b. What happens to the average rate of change of the flow rate as the pressure increases?

Solution :

a) 

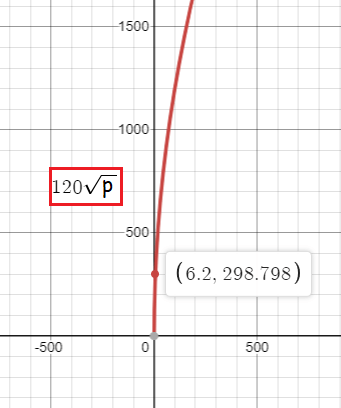
When the pressure is more than 6.2 the flow rate exceeds more than 300 gallons per minute.

b) By tracing the points on the curve, we know that when the pressure increases, the flow also increase.

Problem 4 :

The speed s (in meters per second) of a long jumper before jumping can be modeled by the function s = 10.9 √h , where h is the maximum height (in meters from the ground) of the jumper.

Use a graphing calculator to graph the function. A jumper is running 9.2 meters per second. Estimate the maximum height of the jumper.

Solution :

a)

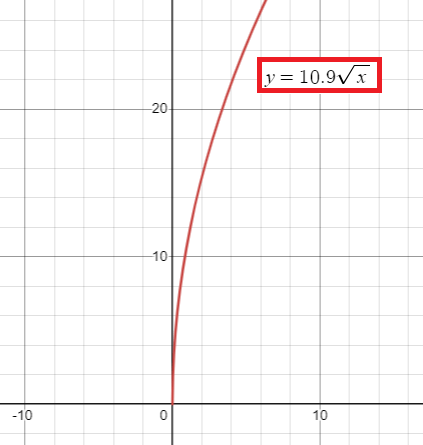
 s = 10.9 √h

When s = 9.2

9.2 = 10.9 √h

√h = 9.2/10.9

√h = 0.844

h = (0.844)²

h = 0.7123 m

So, the maximum height of the jumper is 0.71 m.

Problem 5 :

The velocity v (in meters per second) of a tsunami can be modeled by the function v(x) = √(9.8x)  , where x is the water depth (in meters).

(a) Use a graphing calculator to graph the function. At what depth does the velocity of the tsunami exceed 200 meters per second?

(b) What happens to the average rate of change of the velocity as the water depth increases?

Solution :

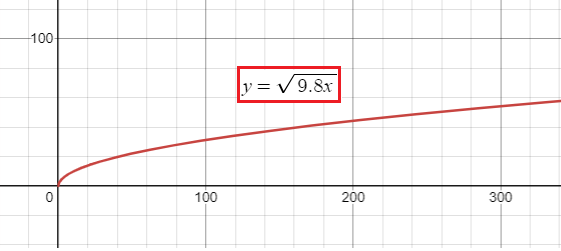
a)  The velocity exceeds 200 meters per second at a depth of about 4090 meters.

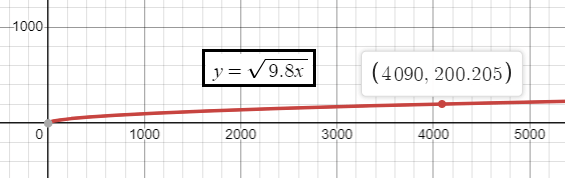
b)  Calculating the average rate of change over the interval x = 0 to x = 1000

The average rate of change of the velocity decreases as the water depth increases.