COMPARE AND INTERPRET THE CONSTANT OF PROPORTIONALITY

Give the slope of the graph and the unit rate.

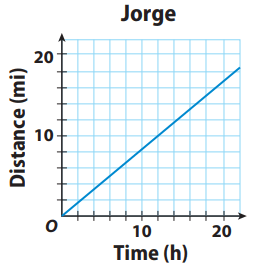
Problem 1 :

Jorge: 5 miles every 6 hours

Solution :

From the given statement :

Jorge: 5 miles every 6 hours

k = 5/6

From the given graph :

Choosing one of the points from the line, say (12, 10)

k = 10/12

k = 5/6

Problem 2 :

A supply company sell packs of paper by the box. Each box contains the same number of packs of paper, P. Which equation can be used to find the total number of of packs of paper, T, that would be in B boxes ordered ?

a) B + P = T     b)  P/B = T     c)  BP = T     d) B/P = T

Solution :

Number of papers in each pack = P

Number of boxes ordered = B

Total number of packs T = BP

So, option c is correct.

Problem 3 :

Which equation could be used to find the number of days d in h hours ?

a) 24/h = d     b)  24 + h = d     c)  24h = d     d) h/24 = d

Solution :

1 day = 24 hours

1 hour = 1/24 days

h hour = h(1/24) days

h hours = h/24

d = h/24

So, option d is correct.

Problem 4 :

The graph below shoes how much plant grew monthly.

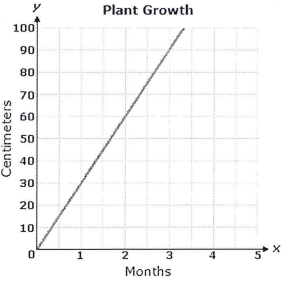
Based on the graph, what does the point (2, 60) represent ?

a) The plant grew 2 cm in 60 months.

b) The plant grew 60 cm in 2 months.

c)  The plant grew 30 cm in 2 months.

d) The plant grew 60 cm in 2 days.

Solution :

x-axis represents, number of months

y- axis represents, number of centimeters.

Choosing one of the points from the graph, say (2, 60)

It grew 60 cm in 2 months.

Problem 5 :

Russell conducted an experiment where he collected snow in container, measured it, then measured the amount of water in the container after the snow had melted. He created the graph below to display his findings. 

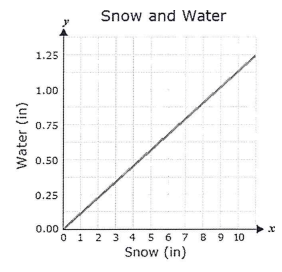
Based on the graph, what does the point (0, 0) represent ?

a) The collection of 0 inches of snow results in no water.

b) The collection of 0 inches of water results in no snow.

c) The amount of snow was not proportional to the amount of water.

Solution :

The collection of 0 inches of snow results in no water.

Problem 6 :

Each table represents a proportional relationship. For each, find the constant of proportionality, and write an equation that represents the relationship.

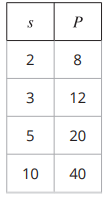
Solution :

When s = 2, P = 8

When s = 3, P = 12

Constant of proportionality (k) = y/x ==> P/s

k = 8/2

k = 4

Equation represented by the relationship

P = 4s

Problem 7 :

A recipe says that 2 cups of dry rice will serve 6 people. Complete the table as you answer the questions.

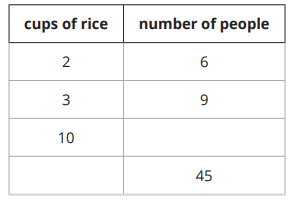
a. How many people will 10 cups of rice serve?

b. How many cups of rice are needed to serve 45 people?

Solution :

Number of cups of rice (x) = 2,

number of people served (y) = 6

Constant of proportionality (k) = 6/2

k = 3

Equation represented by the table :

y = 3x

If x = 10, then y = 3(10) ==> 30

If y = 45, then x = 45/3 ==> 15

a. So, 10 cups of rice can be served for 30 people.

b. So, 15 cups of rice is needed.

Problem 8 :

A recipe says that 2 cups of dry rice will serve 6 people. Complete the table as you answer the questions.

a. How many people will 1 cup of rice serve?

b. How many people will 3 cups of rice serve? 12 cups? 43 cups?

c. How many people will x cups of rice serve?

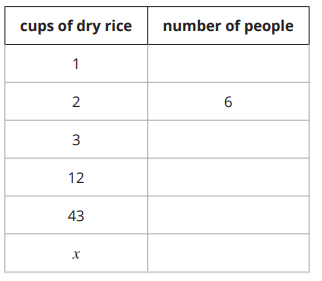
Solution :

Cups of dry rice (x), number of people (y).

2 cups of rice will be served for 6 people.

Constant of proportionality (k) = 6/2

k = 3

y = 3x

When x = x, then y = 3x

Problem 9 :

A factory produces widgets at a constant rate. After 4 hours, 3,120 widgets have been produced. At what rate are the widgets being produced?

a) 630 widgets per hour       b) 708 widgets per hour

c) 780 widgets per hour       d) 1,365 widgets per hour

Solution :

Quantity of widgets = 3120

Time taken = 4 hours

1 hour = 3120/4

1 hour = 720 widgets

So, option c is correct.

Problem 10 :

There are 3 cans that store 9 tennis balls. Consider the number of balls per can.

a) Find the constant of proportionality for this situation.

b) What does it mean for this situation?

c) Write an equation to represent the relationship.

Solution :

3 cans will store = 9 balls

1 can will store = 9/3

= 3 balls.

Constant of proportionality = 3

b) Each can will store 3 balls.

c) Equation y = 3x