COMBINING TRANSFORMATIONS OF FUNCTIONS WORD PROBLEMS

Problem 1 :

A cable company charges customers $60 per month for its service, with no installation fee. The cost to a customer is represented by

c(m) = 60m

where m is the number of months of service.

To attract new customers, the cable company reduces the monthly fee to $30 but adds an installation fee of $45. The cost to a new customer is represented by

r(m) = 30m + 45

where m is the number of months of service. Describe the transformations from the graph of c to the graph of r.

Solution :

c(m) = 60m and r(m) = 30m + 45

Thinking about the relationship between 60m and 30m, by dividing 60m by 2 we get 30m.

So, the multiplication factor will be 1/2. Since 1/2 is in between 0 and 1 and it is multiplied by the input, it should be vertical shrink with the factor of 1/2.

After done vertical shrink, there is a translation of 45 units up.

Describing the transformations :

Vertical shrink with the factor of 1/2 and translating the curve up 45 units.

Problem 2 :

The total cost C (in dollars) to cater an event with p people is given by the function

C(p) = 18p + 50

The set-up fee increases by $25. The new total cost T is given by the function

T(p) = C(p) + 25

Describe the transformation from the graph of C to the graph of T.

Solution :

T(p) = C(p) + 25

C(p) = 18p + 50

Applying the value of C(p), we get

Finding the new function :

T(p) = (18p + 50) + 25

= (18p + 50) + 25

T(p) = 18p + 75

Describing the transformations :

C(p) is translating up 25 units vertically.

Problem 3 :

You and a friend start biking from the same location. Your distance d (in miles) after t minutes is given by the function

d(t) = (1/5) t

Your friend starts biking 5 minutes after you. Your friend’s distance f is given by the function

f(t) = d(t − 5)

Describe the transformation from the graph of d to the graph of f

Solution :

Comparing d(t) and d(t - 5), it is clear that we have to move the graph horizontally 5 units to the right.

d(t) = (1/5) t

d(t - 5) = (1/5) (t - 5)

= (t - 5)/5

= (1/5) t - 5/5

= (1/5) t - 1

Coordinates of d(t) :

(5, 1) (10, 2) and (15, 3)

Coordinates of d(t - 5) :

(5, 0) (10, 1) and (15, 2)

For every 5 minutes, your friend will be 1 mile away from you.

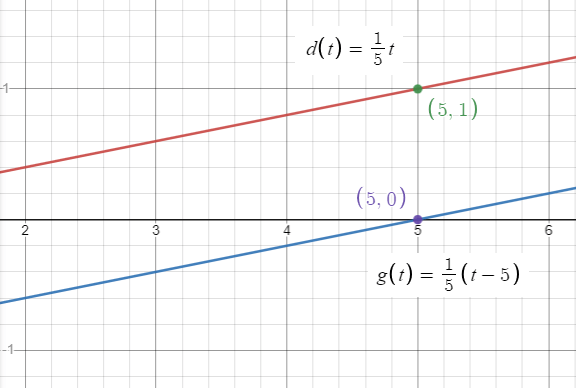
Problem 4 :

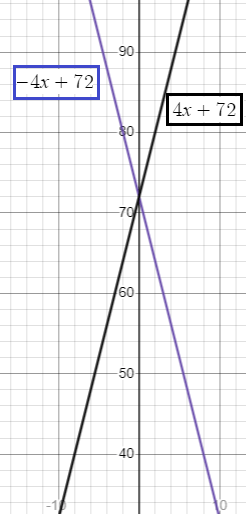
The function

t(x) = −4x + 72

represents the temperature from 5 P.M. to 11 P.M., where x is the number of hours after 5 P.M. The function

d(x) = 4x + 72

represents the temperature from 10 A.M. to 4 P.M., where x is the number of hours after 10 A.M. Describe the transformation from the graph of t to the graph of d.

Solution :

t(x) = −4x + 72 and d(x) = 4x + 72

In the function f(x), applying x as -x

t(-x) = -4(-x) + 72

t(-x) = 4x + 72

d(x) is reflection of the graph of t(x) with respect to y-axis.

Problem 5 :

A school sells T-shirts to promote school spirit. The school’s profit is given by the function

P(x) = 8x − 150

where x is the number of T-shirts sold. During the play-offs, the school increases the price of the T-shirts. The school’s profit during the play-offs is given by the function

Q(x) = 16x − 200

where x is the number of T-shirts sold. Describe the transformations from the graph of P to the graph of Q

Solution :

P(x) = 8x − 150 and Q(x) = 16x − 200

2 P(x) - 50 = 2(8x) - 150 - 50

Vertical stretch with the factor of 2 and translation vertically 50 units.

Problem 6 :

The graph of

f(x) = x + 5

is a vertical translation 5 units up of the graph of f(x) = x.

How can you obtain the graph of

f(x) = x + 5

from the graph of f(x) = x using a horizontal translation?

Solution :

f(x) = x - (-5)

Horizontal translation of 5 units left.

Problem 7 :

When is the graph of y = f(x) + w the same as the graph of y = f(x + w) for linear functions? Explain your reasoning.

Solution :

y = f(x) + w

y = f(x + w)

The above two functions will not have same graph.

In the function y = f(x) + w, w is the number of units of vertical translation. If w is positive, we have to move up. If w is negative, we have to move down.

Here y = f(x + w), w have to understand it as f(x - (-w))

Here -w tells us, we have to move the graph horizontally w units left.