CLASSIFYING TRIANGLES BY SIDES LENGTHS ACUTE OBTUSE OR RIGHT

State if each triangle is acute, obtuse, or right.

Problem 1 :

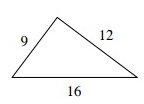
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

16² ? 9² + 12²

256 ? 81 + 144

256 > 225

Because c² is greater than a² + b², the triangle is obtuse.

Problem 2 :

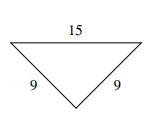
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

15² ? 9² + 9²

225 ? 81 + 81

225 > 162

Because c² is greater than a² + b², the triangle is obtuse.

Problem 3 :

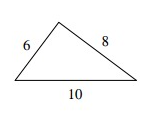
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

10² ? 6² + 8²

100 ? 36 + 64

100 = 100

Because c² is equal to a² + b², the triangle is right.

Problem 4 :

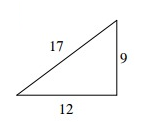
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

17² ? 12² + 9²

289 ? 144 + 81

289 > 225

Because c² is greater than a² + b², the triangle is obtuse.

Problem 5 :

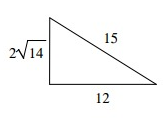
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

15² ? 12² + (2√14)²

225 ? 144 + 56

225 > 200

Because c² is greater than a² + b², the triangle is obtuse.

Problem 6 :

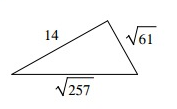
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

(√257)² ? 14² + (√61)²

257 ? 196 + 61

257 = 257

Because c² is equal to a² + b², the triangle is right.

Problem 7 :

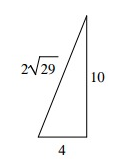
Solution:

Let c represent the length of the longest side of the triangle. 

c² ? a² + b²

(2√29)² ? 4² + 10²

116 ? 16 + 100

116 = 116

Because c² is equal to a² + b², the triangle is right.

Problem 8 :

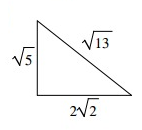
Solution:

Let c represent the length of the longest side of the triangle. 

c2 ? a2 + b2

(√13)² ? (√5)² + (2√2)²

13 ? 5 + 8

13 = 13

Because c² is equal to a² + b², the triangle is right.