CLASSIFYING LINES FROM THE GIVEN EQUATIONS

If two lines are travelling in the same path, then the lines are parallel. Slopes of the lines can be considered as m₁ and m₂

If two lines are parallel, then their slopes will be equal.

m₁ = m₂

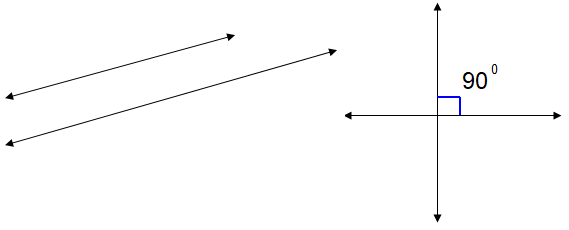
If two lines are perpendicular, then the product of their slopes is equal to -1

m₁ x m₂ = -1

Problem 1 :

Classify the pair of equations.

-3x + y = 11

y - 29 = 3(x - 6)

i)  The same line 

ii) Distinct parallel lines

iii) Perpendicular lines

iv) Intersecting but not perpendicular lines

Solution :

Given, -3x + y = 11 and y - 29 = 3(x - 6)

-3x + y = 11

y = 3x + 11

Slope intercept equation of a line y = mx + b, we get

m = slope

m₁ = 3

y - 29 = 3(x - 6)

y - 29 = 3x - 18

y = 3x - 18 + 29

y = 3x + 11

m₂ = 3

The slopes are m₁ = 3 and m₂ =  3.

Since, the slope of the lines m₁ and m₂ are parallel.

So, option ii) is correct.

Problem 2 :

Classify the pair of equations.

-x + y = 8

y - 5 = (x + 3)

Solution :

Given, -x + y = 8 and y - 5 = (x + 3)

-x + y = 8

y = x + 8

Slope intercept equation of a line y = mx + b, we get

m = slope

m₁ = 1

y - 5 = (x + 3)

y = 5(x + 3) 

y = 5x + 15

m₂ = 5

The slopes are m₁ = 1 and m₂ =  5.

Since, the slope of the lines m₁ and m₂ are neither.

Problem 3 :

Classify the pair of equations.

3x + 2y = -20

y + 22 = -3/2(x - 8)

Solution :

Given, 3x + 2y = -20 and y + 22 = -3/2(x - 8)

3x + 2y = -20

2y = -3x - 20

Slope intercept equation of a line y = mx + b, we get

m = slope

m₁ = -3/2

m₂ = -3/2

The slopes are m₁ = -3/2 and m₂ =  -3/2.

Since, the slope of the lines m₁ and m₂ are parallel.

Problem 4 :

Classify the pair of equations.

-x + 5y = -5

5x + y = 48

Solution :

Given, -x + 5y = -5 and 5x + y = 48

-x + 5y = -5

5y = x - 5

Slope intercept equation of a line y = mx + b, we get

m = slope

m₁ = 1/5

5x + y = 48

y = - 5x + 48

m₂ = -5

The slopes are m₁ = 1/5 and m₂ =  -5.

= 1/5 × -5

= -1

Since, the slope of the lines m₁ and m₂ are perpendicular.

Problem 5 :

Classify the pair of equations.

-8x - 9y = -27

24x + 27y = 81

Solution :

Given, -8x - 9y = -27 and 24x + 27y = 81

-8x - 9y = -27

-9y = 8x - 27

9y = -(8x - 27)

9y = -8x + 27

Slope intercept equation of a line y = mx + b, we get

m = slope

m₁ = -8/9

24x + 27y = 81

27y = -24x + 81

m₂ = -8/9

The slopes are m₁ = -8/9 and m₂ =  -8/9.

Since, the slope of the lines m₁ and m₂ are parallel.

Problem 6 :

Classify the pair of equations.

9x - 10y = -10

-9x + 10y = 10

Solution : 

Given, 9x - 10y = -10 and -9x + 10y = 10

9x - 10y = -10

-10y = -9x - 10

10y = -(-9x - 10)

10y = 9x + 10

Slope intercept equation of a line y = mx + b, we get

m = slope

m₁ = 9/10

-9x + 10y = 10

10y = 9x + 10

m₂ = 9/10

The slopes are m₁ = 9/10 and m₂ =  9/10.

Since, the slope of the lines m₁ and m₂ are parallel.