CHORD CHORD PRODUCT THEOREM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The products of the lengths of the line segments on each chord are equal.
Proof :
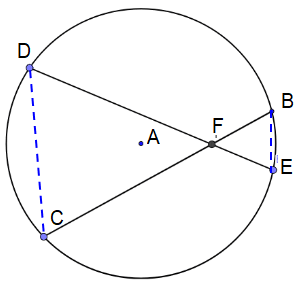
Considering the chords BC and DE,
∠DFC = ∠BFE (vertically opposite angles)
∠CDE = ∠CBE (angle between same arc CE)
∠DCB = ∠DEB (angle between same arc DB)
Triangles FDC and FBE are similar, then
CF/FE = DF/BF
Doing cross multiplication, we get
CF ⋅ BF = DF ⋅ EF
For each
figure, determine the value of the variable and the indicated lengths by
applying the chord-chord product theorem.
Problem 1:
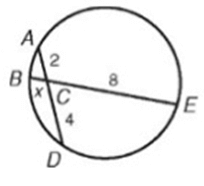
Find the following.
i) x ii) AD and iii) BE
Solution :
Intersecting chord theorem,
CA ∙ CD = CB ∙ CE
2 ∙ 4 = x ∙ 8
8 = 8x
x = 1
|
AD = CA + CD AD = 2 + 4 AD = 6 |
BE = CB + CE = x + 8 = 1 + 8 BE = 9 |
Problem 2 :
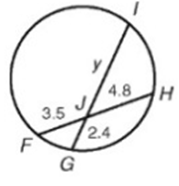
Find the following.
i) y ii) FH and iii) GL
Solution :
Intersecting chord theorem,
JG ∙ JI = JF ∙ JH
2.4 ∙ y = 3.5 ∙ 4.8
2.4y = 16.8
y = 16.8/2.4
y = 7
|
FH = JF + JH = 3.5 + 4.8 FH = 8.3 |
GI = JG + JI = 2.4 + y = 2.4 + 7 GI = 9.4 |
Problem 3 :
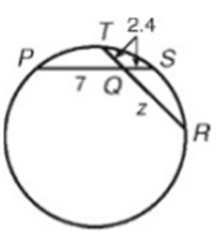
Find the following.
i) z ii) PS and iii) TR
Solution :
Intersecting chord theorem,
QT ∙ QR = QP ∙ QS
2.4 ∙ z = 7 ∙ 2.4
2.4z = 16.8
z = 16.8/2.4
z = 7
|
PS = QP + QS = 7 + 2.4 PS = 9.4 |
RT = QR + QT = z + 2.4 = 7 + 2.4 RT = 9.4 |
Problem 4 :
Find m.
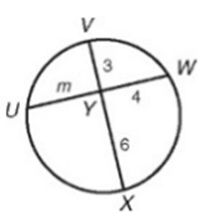
Solution :
Intersecting chord theorem,
YU ∙ YW = YV ∙ YX
m ∙ 4 = 3 ∙ 6
4m = 18
m = 18/4
m = 4.5
|
UW = YU + YW = m + 4 = 4.5 + 4 UW = 8.5 |
VX = YV + YX = 3 + 6 VX = 9 |
Problem 5 :
Find x.
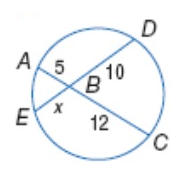
Solution :
Intersecting chord theorem,
BA ∙ BC = BD ∙ BE
5 ∙ 12 = 10 ∙ x
60 = 10x
x = 60/10
x = 6
Problem 6 :
Solve for x.
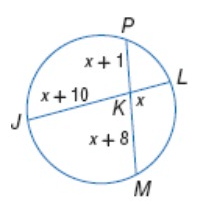
Solution :
Intersecting chord theorem,
KJ ∙ KL = KP ∙ KM
(x + 10) ∙ (x) = (x + 1) ∙ (x + 8)
x² + 10x = x² + 9x + 8
x² - x² + 10x - 9x = 8
x = 8
Problem 7 :
Solve for x.
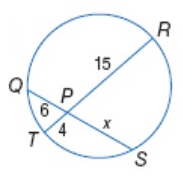
Solution :
Intersecting chord theorem,
PT ∙ PR = PQ ∙ PS
4 ∙ 15 = 6 ∙ x
60 = 6x
x = 60/6
x = 10
Problem 8 :
Solve for x.
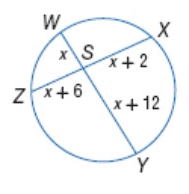
Solution :
Intersecting chord theorem,
SX ∙ SZ = SW ∙ SY
(x + 2) ∙ (x + 6) = x ∙ (x + 12)
x² + 8x + 12 = x² + 12x
4x = 12
x = 12/4
x = 3
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling