CALCULUS AB DERITVATIVE PRACTICE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
If y = x sin x, then dy/dx
A) sin x + cos x B) sin x + x cos x C) sin x - x cos x
D) x(sin x + cos x) E) x(sin x - cos x)
Solution :
y = x sin x
To find the derivative, we use the product rule.
u = x and v = sin x
u' = 1 and v' = cos x
dy/dx = x cos x + sin x (1)
dy/dx = x cos x + sin x
So, option B is correct.
Problem 2 :
Let f be the function given by f(x) = 300x - x3. On which intervals is the function f increasing ?
A) (-∞, -10] and [10, ∞) B) [-10, 10] C) [0, 10] only
D) [0, 10√3] only E) [0, ∞)
Solution :
f(x) = 300x - x3
f'(x) = 300(1) - 3x2
f'(x) = 3(100 - x2)
f'(x) = 0
3(100 - x2) = 0
100 - x2 = 0 or (10 + x) (10 - x) = 0
x = -10 and 10
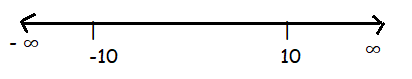
|
(-∞, -10) (-10, 10) (10, ∞) |
f'(x) - + - |
Increasing/decreasing Decreasing Increasing Decreasing |
Increasing --> Positive slope [f'(x) > 0]
At [-10, 10], the function f(x) is having positive slope. So, option B is correct.
Problem 3 :
If f(x) = 7x - 3 + ln x, then f'(1) = ?
A) 4 B) 5 C) 6 D) 7 E) 8
Solution :
f(x) = 7x - 3 + ln x
f'(x) = 7(1) - 0 + 1/x
f'(x) = 7 + 1/x
f'(1) = 7 + 1/1 ==> 8
So, option E will be correct.
Problem 4 :
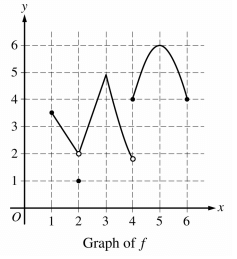
Solution :
In option C, the limit does not exists. So, option C is correct.
Problem 5 :
If y = (x3 - cos x)5, then find y'
A) 5(x3 - cos x)4 B) 5(3x2 + sin x )4
C) 5(3x2 + sin x) D) 5(3x2 + sin x)4 (6x + cos x)
E) 5(x3 - cos x)4 (3x2 + sin x)
Solution :
y = (x3 - cos x)5
Using chain rule, we find the derivative.
y' = 5(x3 - cos x)4 (3x2 - (-sin x))
y' = 5(x3 - cos x)4 (3x2 + sin x)
So, option E is correct.
Problem 6 :
If
f(x) = √(x2-4) and g(x) = 3x-2
then find the derivative of f((g(x)) at x = 3
A) 7/√5 B) 14/√5 C) 18/√5 D) 15/√21 E) 30/√21
Solution :
f(x) = √(x2 - 4) and g(x) = 3x - 2
f(g(x)) = √((3x - 2)2 - 4)
= √[(3x)2 - 2(3x)(2) + 22 - 4]
= √(9x2 - 12x)
[f(g(x))]' = [1/2√(9x2 - 12x)] (18x - 12)
= [1/2√(9x2 - 12x)] (18x - 12)
[f(g(x))]' at x = 3 :
= [1/2√(81 - 36)] (54 - 12)
= [21/√45]
= 21/3√5
= 7/√5
So, option A is correct.
Problem 7 :
The function f is defined by f(x) = x/(x + 2). What points (x, y) on the graph of f have the property that the line tangent to f at (x, y) has slope 1/2 ?
A) (0, 0) only B) (1/2, 1/5) only C) (0, 0) and (-4, 2)
D) (0, 0) and (4, 2/3) E) There are no such points
Solution :
|
When x = 0 y = 0/2 y = 0 |
When x = -4 y = -4/(-2) y = 2 |
So, the points are (0, 0) and (-4, 2). Then option C is correct.
Problem 8 :
Let f(x) = (2x+1)3 and let g be the inverse function of f. Given that f(0) = 1, what is the value of g'(1) ?
A) -2/27 B) 1/54 C) 1/27 D) 1/6 E) 6
Solution :
Given f(0) = 1
0 = f-1(1)
g is the function inverse of f, g(1) = 0.
f(x) = (2x+1)3
f'(x) = 3(2x+1)2 (2)
f'(x) = 6(2x+1)2
f'(0) = 6
f'(f-1(1)) = 6
f'(g(1)) = 6
g(1) = 1/f'(g(1))
g(1) = 1/6
So, option D is correct.
Problem 9 :
Let f be the function defined by f(x) = ln x/x. What is absolute maximum value of f ?
A) 1 B) 1/e C) 0 D) -e
E) f does not have an absolute maximum value
Solution :
f(x) = ln x/x
f'(x) = [x(1/x) - ln x(1)] / x2
f'(x) = [1 - ln x] / x2
f'(x) = 0
1 - ln x = 0
ln x = 1
x = e
Since the given function involves ln, we are allowed to use positive values only.
(0, e), (e, ∞)
x = 1 ∈ (0, e) ==> f'(1) = [1 - ln 1] / 12 ==> 1 > 0
x = 3 ∈ (e, ∞) ==> f'(4) = [1 - ln 4] / 42 ==> - < 0
Drawing the sign diagram, we get
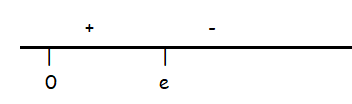
There should be absolute maximum at x = e
Maximum Value :
f(e) = ln e/e
f(e) = 1/e
So, the maximum value is 1/e.
Problem 10 :
Let g be the function given by g(x) = x2 ekx, where k is a constant. For what value of k does g have critical point at x = 2/3 ?
A) -3 B) -3/2 C) -1/3 D) 0 E) There is no such k.
Solution :
g(x) = x2 ekx
u = x2 and v = ekx
u' = 2x and v' = kekx
g'(x) = x2(kekx) + ekx (2x)
g'(x) = xekx (kx + 2]
g'(x) = 0 at x = 2/3
(2/3)ek(2/3) [k(2/3) + 2] = 0
|
ek(2/3) = 0 k(2/3) = ln0 2k/3 = 1 k = 3/2 |
2k/3 + 2 = 0 2k/3 = -2 k = -2(3/2) k = -3 |
So, option A is correct.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling