CALCULATE MISSING FREQUENCY WHEN MEAN IS GIVEN

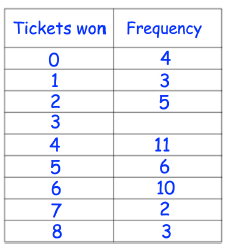
Problem 1 :

Aidan plays 50 games in an arcade. The table shows how many tickets he won in each game.

(a) Work out the missing frequency

(b) Work out the total number of tickets won

(c) Work out the mean number of tickets won per game.

Aidan wants to exchange his ticket for a prize that costs 800 tickets.

(d) How many more games do you expect Aidan would have to play?

Solution :

Let x be the missing frequency.

a) Total number of games played = 50

4 + 3 + 5 + x + 11 + 6 + 10 + 2 + 3 = 50

12 + x + 32 = 50

44 + x = 50

x = 50 - 44

x = 6

b) Number of tickets won =

0(4) + 1(3) + 2(5) + 3x + 4(11) + 5(6) + 6(10) + 7(2) + 8(3)

= 0 + 3 +10 + 3x + 44 + 30 + 60 + 14 + 24

= 13 + 3x + 172

= 185 + 3x

= 185 + 3(6)

= 185 + 18

= 203

c)  Mean number of tickets = 203 / 50

= 4.06

d)  800 - 203

= 597

= 597/4.06

= 147

Expected number of games = 147.

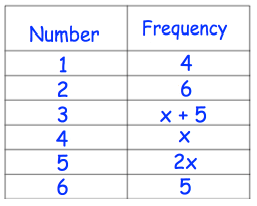
Problem 2 :

Max rolls a dice 80 times. The table shows the results.

(a) Find the value of x

(b) Work out the mean score

Solution :

Number of times he rolls the dice = 80

4 + 6 + x + 5 + x + 2x + 5 = 80

20 + 4x = 80

4x = 80 - 20

4x = 60

x = 60/4

x = 15

b) Mean = 80/6

= 13.3

Problem 3 :

A student was asked to find the arithmetic mean of the numbers 3, 11, 7, 9, 15, 13, 8, 19, 17, 21, 14 and x. He found the mean to be 12. What should be the number in the place of x ?

Solution :

Mean = 12

(3+11+7+9+15+13+8+19+17+21+14+x) / 12 = 12

137 + x = 144

x = 144 - 137

x = 7

Problem 4 :

The average of 2, 7, 6 and x is 5 and the average of 18, 1, 6, x and y is 10. What is the value of y.

Solution :

Let {2, 7, 6, x} be the first data set

Average = 5

(2 + 7 + 6 + x)/4 = 5

15 + x = 20

x = 20 - 15

x = 5

Let {18, 1, 6, x and y is 10} be the second data set.

(18 + 1 + 6 + x + y + 10)/6 = 10

35 + x + y = 60

Applying the value of x,

35 + 5 + y = 60

40 + y = 60

y = 60 - 40

y = 20

So, the missing values are x = 5 and y = 20.

Problem 5 :

If the mean of 5 observations x, x + 2, x + 4, x + 6 and x + 8 is 11, then the mean of the last three observation is.

Solution :

Mean of 5 observations = 11

(x + x + 2 + x + 4 + x + 6 + x + 8) / 5 = 11

5x + 20 = 55

5x = 55 - 20

5x = 35

x = 35/5

x = 7

Mean of last three observations :

= (x + 4 + x + 6 + x + 8)/3

= (3x + 18)/3

= [3(7) + 18] / 3

= (21 + 18)/3

= 39/3

= 13

Problem 6 :

The mean of the following frequency distribution is 25.2. Find the missing frequency x.

Solution :

Total frequency = 8 + x + 10 + 11 + 9

= 38 + x

Sum of fx = 40 + 15x + 250 + 385 + 405

= 1080 + 15x

Mean = (1080 + 15x)/(38 + x)

25.2 = (1080 + 15x)/(38 + x)

25.2(38 + x) = 1080 + 15x

957.6 + 25.2x = 1080 + 15x

25.2x - 15 = 1080 - 957.6

10.2x = 122.4

x = 122.4/10.2

x = 12

So, the missing frequency is 12.

Problem 7 :

Find the missing frequency: mean = 50, Total frequency = 120.

Solution :

Mean = 50

Total frequency = 120

17 + f₁ + 32 + f₂ + 19 = 120

68 + f₁ + f₂ = 120

 f₁ + f₂ = 120 - 68

 f₁ + f₂ = 52 -----(1)

Mean = (170 + 30f₁ + 1600 + 70f₂ + 1710) / Total frequency

50 = (3480 + 30f₁ + 70f₂)/120

50(120) = 3480 + 30f₁ + 70f₂

6000 = 3480 + 30f₁ + 70f₂

6000 - 3480 = 30f₁ + 70f₂

2520 = 30f₁ + 70f₂

Dividing by 10, we get

252 = 3f₁ + 7f₂

3f₁ + 7f₂ = 252 -----(2)

(1) ⋅ 3 ==>  3f₁ + 3f₂ - (3f₁ + 7f₂) = 156 - 252

3f₂ - 7f₂ = -96

-4f₂ = -96

f₂ = 96/4

f₂ = 24

Applying the value of f₂ in (1), we get

 f₁ + 24 = 52

 f₁ = 52 - 24

 f₁ = 28

So, the missing frequencies are 28 and 24 respectively.