AREA OF TRIANGLE WORD PROBLEMS

Problem 1 :

Calculate the area of the triangle.

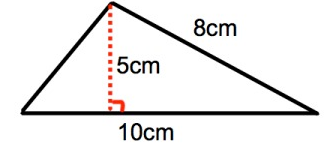
Solution :

area of triangle = 1/2 × b × h

Base (b) = 10 cm

Height (h) = 5 cm

= 1/2 × 10 × 5

= 5 × 5

= 25 cm²

So, the area of a triangle is 25 cm².

Problem 2 :

A triangle has base length of 14 cm. The perpendicular height is 9 cm. Find the area of the triangle. 

Solution :

area of triangle = 1/2 × b × h

Base (b) = 14 cm

Height (h) = 9 cm

= 1/2 × 14 × 9

= 7 × 9

= 63 cm²

So, the area of a triangle is 63 cm².

Problem 3 :

Work out the area of the right - angled triangle.

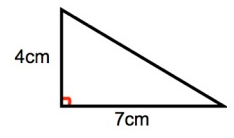
Solution :

area of triangle = 1/2 × b × h

Base (b) = 7 cm

Height (h) = 4 cm

= 1/2 × 7 × 4

= 7 × 2

= 14 cm²

So, the area of a triangle is 14 cm².

Problem 4 :

The area of the triangle is 20 cm², find x.

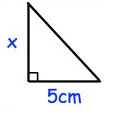
Solution :

area of triangle = 1/2 × b × h

area of triangle = 20 cm²

Base (b) = 5 cm

Height (h) = x

20 = 1/2 × 5 × x

x = (20 × 2)/5

x = 40/5

x = 8 cm

Problem 5 :

The area of the triangle is 30 cm², find y.

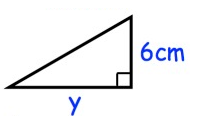
Solution :

area of triangle = 1/2 × b × h

area of triangle = 30 cm²

Base (b) = y

Height (h) = 6 cm

30 = 1/2 × y × 6

y = (30 × 2)/6

y = 60/6

y = 10 cm

Problem 6 :

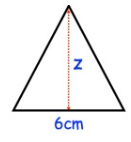
The area of the triangle is 12 cm², find z.

Solution :

area of triangle = 1/2 × b × h

area of triangle = 12 cm²

Base (b) = 6 cm

Height (h) = z

12 = 1/2 × 6 × z

z = (12 × 2)/6

z = 24/6

z = 4 cm

Problem 7 :

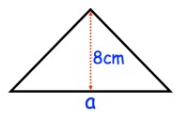
The area of the triangle is 56 cm², find a.

Solution :

area of triangle = 1/2 × b × h

area of triangle = 56 cm²

Base (b) = a

Height (h) = 8 cm

56 = 1/2 × a × 8

a = (56 × 2)/8

a = 112/8

a = 14 cm²

Problem 8 :

The diagram below shows a farmer's field.

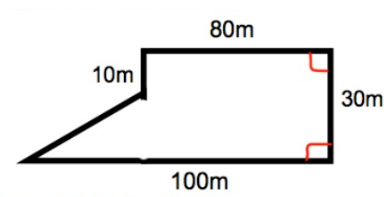
The farmer wants to plant a new crop. Each sack of seed covers 30m². The cost of each sack is $6.

Work out the cost to buy enough seed to cover the field.

Solution :

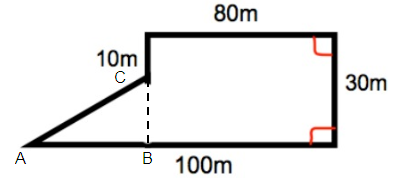
Area of rectangle = l × w

length = 80 m

width = 30 m

Area of rectangle = 80 × 30

= 2400 m²

Area of triangle = 1/2 × b × h

= 1/2 × 20 × 20

= 400/2

= 200 m²

Total area = area of rectangle + area of triangle

= 2400 + 200

= 2600 m²

Each sack of seed covers 30 m²

= 2600/30

= 86.6

= 87

Cost of each sack = $6

So, 87 sack cost = 87 × 6

= $522

Problem 9 :

ABCD and WXYZ are squares.

Calculate the area of the shaded square WXYZ.

Solution :

By observing the figure,

Using Pythagorean theorem

WZ² = AZ² + AW²

WZ²= 8² + 2² 

= 64 + 4

WZ² = 68

WZ = √68

Squaring on each sides. 

(WZ)² = (√68)²

(WZ)² = 68 cm

So, the area of the shaded square WXYZ is 68 cm.

Problem 10 :

The diagram below shows a garden.

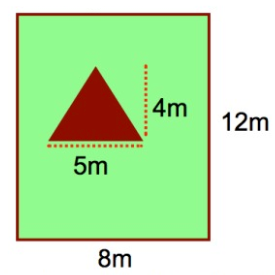
The garden has a triangular vegetable patch and the rest of the garden is grass calculate the area of the garden that is grass.

Solution :

Area of rectangle = l × w

length = 8 m

width = 12 m

Area of rectangle = 8 × 12

= 96 m²

Area of triangle = 1/2 × b × h

base = 5 m

height = 4 m

= 1/2 × 5 × 4

= 20/2

= 10 m²

area of garden = area of rectangle - area of triangle

= 96 - 10

area of garden  = 86 m²

Problem 11 :

A logo consists of a rectangle and an isosceles triangle.

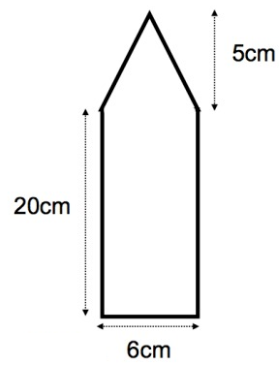
Calculate the area of the logo.

Solution :

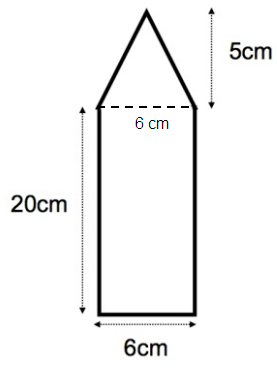
Area of rectangle = l × w

length = 6 cm

width = 20 cm

Area of rectangle = 6 × 20

= 120 cm²

Area of isosceles triangle = 1/2 × b × h

base = 6 cm

height = 5 cm

= 1/2 × 6 × 5

= 30/2

= 15 cm²

area of the logo = area of rectangle  + area of isosceles triangle

= 120 + 15

area of the logo = 135 cm²

So, area of the logo is 135 cm².