AREA OF SIMILAR SOLIDS

If the sides of a rectangle are multiplied by k, a similar rectangle is obtained.

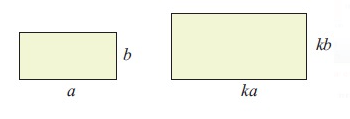
The new area = ka × kb

= k² ab

= k² × the old area

If an object or figure is enlarged by a scale factor of k, then

 the area of the image = k² × the area of the object

Consider the following similar shapes. Find

i) the scale factor

ii) the length or area marked by the unknown. 

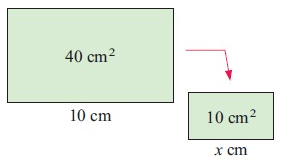
Problem 1 :

Solution :

i) scale factor  :

10 = k² × 40

k² = 10/40

k² = 1/4

k = 1/2

ii) the length :

Length of smaller figure = Scale factor x length of small figure

x = k × 10

x = 1/2 × 10

x = 5 cm

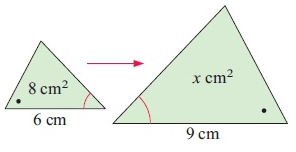
Problem 2 :

Solution :

i) scale factor  :

9 = k × 6

k = 9/6

k = 3/2

Here, we find area of the large figure.

ii) Area :

Area of large shape = k² × Area of smaller shape

x² = k² × 8

By applying the value of k, we get

x² = (3/2)² × 8

= 18 cm²

Area of the large shape is 18 cm².

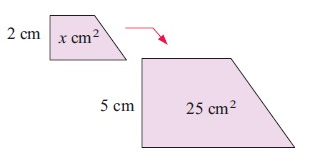
Problem 3 :

Solution :

i) scale factor :

5 = k × 2

k = 5/2

ii)  Area :

Area of large shape = k² × Area of smaller shape

25 = (5/2)² × x

25 = 25x/4

x = 25(4/25)

x = 4 cm²

Problem 4 :

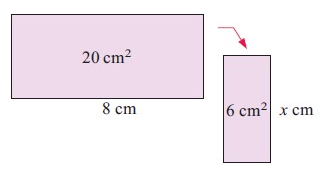
Solution :

i) scale factor :

6 = k² × 20

k² = 6/20

k² = 3/10

k = √3/10

k = √0.3

k ≈ 0.548

ii) the length :

Length of smaller shape = k (length of larger shape)

= k × 8

= 0.548 × 8

≈ 4.38 cm

Problem 5 :

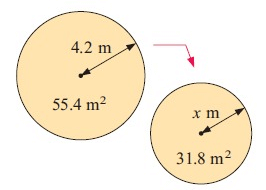
Solution :

i) scale factor :

31.8 = k² × 55.4

k² = 31.8/55.4

k² = 0.574

k = √0.574

k ≈ 0.758

ii) the length or area :

x = k × 4.2

x = 0.758 × 4.2

x ≈ 3.18 m

Problem 6 :

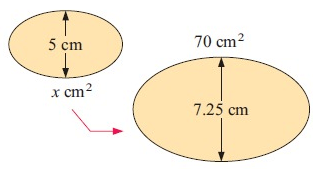
Solution :

i) scale factor :

7.25 = k × 5

k = 7.25/5

k ≈ 1.45

ii)  Area :

Area of the large shape = k² x area of small shape

70 = k² (x)

Applying the value of k, we get

70 = (1.45)² x

x = 70/(1.45)²

x = 70/2.1025

x = 33.29

Approximately 33.3 cm²