AREA OF A SHADED REGION WITH SECTOR OF A CIRCLE AND TRIANGLE

Find the area of the shaded region.

Problem 1 :

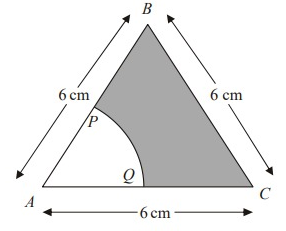
The diagram shows an equilateral triangle ABC with sides of length 6 cm. 

P is the midpoint of AB.

Q is the midpoint of AC.

APQ is a sector of a circle, center A.

Calculate the area of the shaded region.

Give your answer correct to 3 significant figures.

Solution:

So, area of the shaded region is 10.878 cm².

Problem 2 :

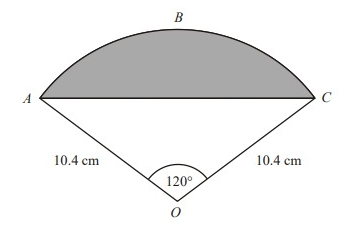
The diagram shows a sector OABC of a circle with centre O.

OA = OC = 10.4 cm

Angle AOC = 120˚

(a) Calculate the length of the arc ABC of the sector. Give your answer correct to 3 significant figures.

(b) Calculate the area of the shaded segment ABC . Give your answer correct to 3 significant figures.

Solution:

a)

The length of arc ABC:

Arc length = 2πr (θ/360°)

= 2 × 3.14 × 10.4(120°/360°)

= 21.771 cm

b)

The area of shaded segment ABC,

Problem 3 :

The diagram shows a sector of a circle with centre O.

The radius of the circle is 8 cm.

PRS is an arc of the circle.

PS is a chord of the circle.

Angle POS = 40˚

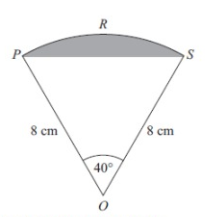
Calculate the area of the shaded segment.

Give your answer correct to 3 significant figures.

Solution:

Hence, area of shaded region is 1.752 cm².

Problem 4 :

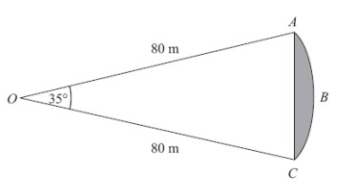
ABC is an arc of a circle centre O with radius 80 m.

AC is a chord of the circle.

Angle AOC = 35˚.

Calculate the area of the shaded region.

Give your answer correct to 3 significant figures.

Solution:

Hence, area of shaded region is 118.756 m².