APPLICATION OF RIGHT TRIANGLE IN TRIGONOMETRY

Solve the problem.

Problem 1 :

A 29 foot water slide has a 17 foot vertical ladder. How far is it along the ground from the end of the slide back to the base of the ladder that leads to the slide?

Solution :

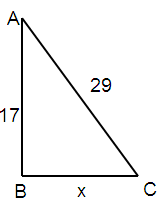
Given, AC = 29 foot

AB = 17 foot

Using Pythagorean Theorem,

AC² = AB² + BC²

29² = 17² + BC²

BC² = 29² - 17²

= √841 - 289

BC = √552

BC = 23.49 ft

So, the base of the ladder is 23.5 ft.

Problem 2 :

A painter leans a 30 foot ladder against one wall of a house. At what height does the ladder touch the wall if the foot of the ladder is 10 ft from the base of the wall?

Solution :

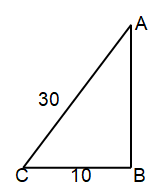
Given, AC = 30 foot

BC = 10 foot

Using Pythagorean Theorem,

AC² = AB² + BC²

30² = AB² + 10²

AB² = 30² - 10²

= √900 - 100

AB = √800

AB = 28.28 ft

So, the height is 28.3 ft.

Problem 3 :

From a distance of 45 feet from the base of a building, the angle of elevation to the top of the building is 68˚. Estimate the height of the building to the nearest foot.

Solution :

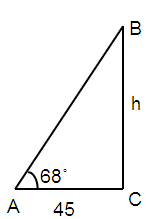
tan 68˚ = h/45

h = 45 × tan 68˚

h = 45 × 2.46

h = 111 feet

So, the height of the building is 111 feet.

Problem 4 :

A kite is currently flying at an altitude of 15 meters above the ground. If the angle of elevation from the ground to the kite is 35˚, find the length of the kite string to the nearest meter.

Solution :

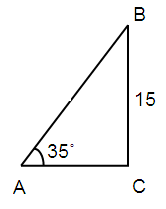
sin θ = opposite / hypotenuse

sin 35˚ = BC/AB

AB = 15/sin 35˚

AB = 15/0.57

AB = 26.3

So, the length of the kite string is 26 meters.

Problem 5  :

From a distance of 1217 feet from a spotlight, the angle of elevation to a cloud base is 43˚. Find the height of the cloud base to the nearest foot.

Solution :

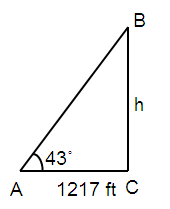
tan θ = opposite / adjacent

tan 43˚ = h/1217

h = tan 43˚/ 1217

h = 0.9325 × 1217

h = 1134.9 ft

So, the height of the cloud base is 1135 ft.

Solve the right triangle using the information given. Round answers to two decimal places, if necessary.

Problem 6 :

b = 8, A = 30˚; Find a, c and B.

Solution :

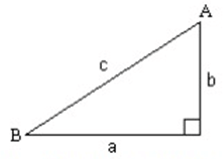
Find c :

cos θ = Adjacent / hypotenuse

cos 30˚ = b/c

0.866 = 8/c

c = 8/0.866

c = 9.24

Find a :

sin θ = Opposite / hypotenuse

sin 30˚ = a/9.24

0.5 = a/9.24

a = 0.5 × 9.24

a = 4.62

Find B:

B = 90˚ - A

B = 90˚ - 30˚

B = 60˚

Problem 7 :

a = 2, A = 40˚; Find b, c and B

Solution :

Find c :

sin θ = Opposite / hypotenuse

sin 40˚ = 2/c

0.642 = 2/c

c = 2/0.642

c = 3.11

Find b :

cos θ = Adjacent / hypotenuse

cos 40˚ = b/c

0.766 = b/3.11

b = 0.766 × 3.11

b = 2.38

Find B :

B = 90˚ - A

B = 90˚ - 40˚

B = 50˚

Problem 8 :

a = 7, b = 4; Find c, A and B.

Solution :

Find c:

Using Pythagorean Theorem,

c² = a² + b²

c² = 7² + 4²

c² = 49 + 16

c = √65

c = 8.06

Find A:

tan A = a/b

tan A = 7/4

A = tan^-1 (7/4)

A = 60.26˚

Find B:

tan B = b/a

tan B = 4/7

B = tan^-1 (4/7)

B = 29.74˚

Problem 9:

a = 4, c = 9; Find b, A and B.

Solution :

Find b:

Using Pythagorean Theorem,

c² = a² + b²

b² = c² - a²

b² = 9² - 4²

b² = 81 - 16

b = √65

b = 8.06

Find A:

sin A = a/c

sin A = 4/9

A = sin^-1 (4/9)

A = 26.39˚

Find B:

cos B = a/c

cos B = 4/9

B = cos^-1 (4/9)B = 63.61˚