APPLICATION OF DERIVATIVES ON AP CALCULUS AB WORKSHEET

Problem 1 :

For what value of x does the function

f(x) = x³ - 9x² - 120x + 6

have a local minimum ?

A)  10     B)  4      C)  -4    D)  -10

Solution

Problem 2 :

Suppose f'(x) = x (x - 2)² (x + 3). which of the following is (are) true ?

I. f has a local maximum at x = -3

II. f has local minimum at x = 0

III. f has neither a local maximum nor local minimum at x = 2

A)  I only     B)  II only     C)  III only     D) I and II only

E)  I, II and III

Solution

Problem 3 :

The maximum value of the function 

f(x) = x⁴ - 4x³ + 6 on [1, 4] is 

A)  1      B)  0      C)  3     D)  6      E)  -27

Solution

Problem 4 :

Find all critical numbers of the function g(x) = x⁴ - 4x²

Solution

Problem 5 :

Locate the absolute extrema of the function

f(x) = x³ - 12x

on the closed interval [0, 4]

A) absolute max (2, -16) and absolute min (4, 16)

B)  no absolute max, absolute min (4, 16)

C)  absolute max (4,16); absolute min (2, -16)

D) Absolute max (4, 16), no absolute min

E) no absolute max or min.

Solution

Problem 1 :

If (x + 2y) (dy/dx) = 2x - y, what is the value of d²y/dx² at the point (3, 0) ?

A)  -10/3      B)  0     C)  2    D) 10/3   E)  Undefined

Solution

Problem 2 :

For t ≥ 0, the position of a particle moving along the x-axis is given by x(t) = sin t - cos t. What is the acceleration of the particle at the point where the velocity is equal to 0 ?

A)  -√2    B)  -1      C)  0      D)  1      E) √2

Solution

Problem 3 :

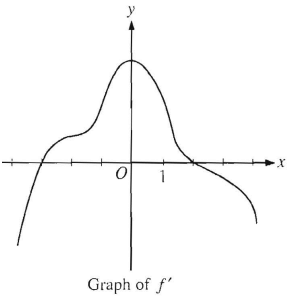
The graph f', the derivative of the function, f is shown above. Which of the following statements must be true ?

I)  f has relative minimum at x = -3

II) The graph of f has a point of inflection at x = -2

III) The graph of f is concave down for 0 < x < 4

A)  I only    B)  II only   C)  III only    D)  I and II only 

E)  I and III only

Solution

Problem 4 :

The graph of y = e^{tan x}- 2 crosses the x-axis at one point in the interval [0, 1]. What is the slope of the graph at this point ?

A)  0.606    B)  2      C) 2.242     D)  2.961    E)  3.747

Solution

Problem 5 :

f'(x) = √(x⁴+1) + x³ - 3x, then f has a local maximum at x = ?

A)  -2.314    B)  -1.332       C)  0.350    D)  0.829     E) 1.234

Solution

Problem 6 :

For -1.5 < x < 1.5, let f be a function with first derivative given by

Which of the following are all intervals on which graph of f is concave down ?

A)  (-0.418, 0.418)      B)  (-1, 1)

C)  (-1.354, -0.409) and (0.409, 1.354)

D)  (-1.5, -1) and (0, 1)

E)  (-1.5, -1.354) (-0.409, 0) and (1.354, 1.5)

Solution

Problem 7 :

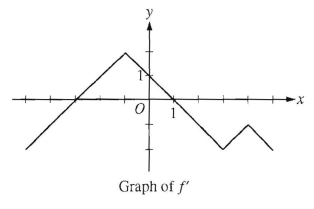
The graph of f', the derivative of f is shown above. The function f has local maximum at x = ?

A)  -3         B)  -1         C)  1         D)  3        E) 4

Solution

Problem 8 :

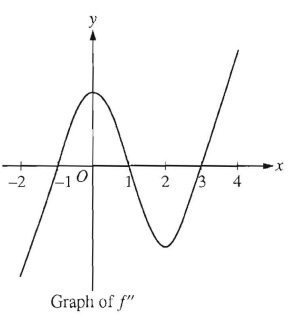
The graph of f'', the second derivative f, is shown above -2 ≤ x ≤ 4. What are all intervals on which the graph of the function f is concave down ?

A)  -1 < x < 1       B)  0 < x < 2      C) 1 < x < 3

D) -2 < x < -1       E)  -2 < x < -1 and 1 < x < 3

Solution

Problem 9 :

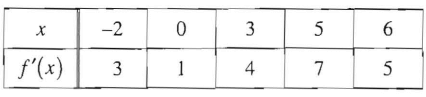
Let f be a polynomial with values of f'(x) at selected values of x given in the table above. Which of the following must be true for -2 < x < 6?

A)  The graph of f is concave up.

B)  The graph of f has at least two points of inflection

C) f is increasing

D)  f has no critical points.

E)  f has at least two relative extrema

Solution

Problem 10 :

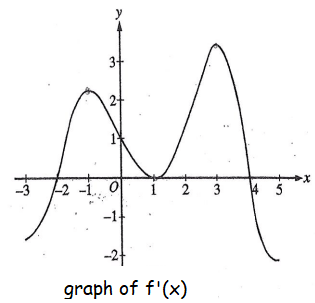
The graph of the derivative of a function f is shown in the figure above. The graph has horizontal tangent lines at x = -1, x = 1 and x = 3. At which of the following values of x does f have a relative maximum ?

A)  -2 only      B)  1 only    C)  4 only    D)  -1 and 3 only

E)  -2, 1 and 4.

Solution