ANGLES IN SAME SEGMENT OF CIRCLE

Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal

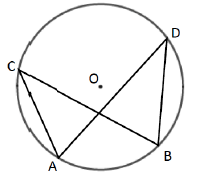
∠ACB = ∠ADB

Problem 1 :

Find the value of x.

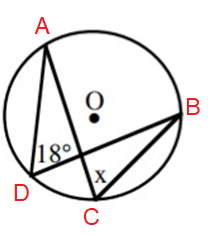
Solution :

∠ADB = ∠ACB (angle between the same arc AB)

So, x = 18

Problem 2 :

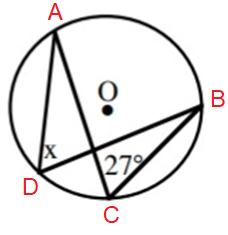
Solution :

∠ADB = ∠ACB (angle between the same arc AB)

So, x = 27

Problem 3 :

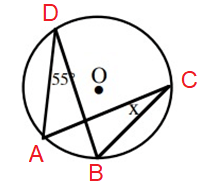
Solution :

∠ADB = ∠ACB (angle between the same arc AB)

So, x = 55

Problem 4 :

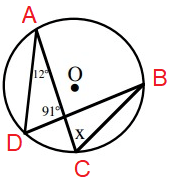
Solution :

x + 12˚ + 91˚ = 180˚

x = 180˚ - (12˚ + 91˚)

x = 180˚ - 103˚

x = 77˚

Problem 5 :

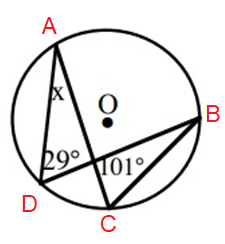
Solution :

x + 29˚ + 101˚ = 180˚

x = 180˚ - (29˚ + 101˚)

x = 180˚ - 130˚

x = 50˚

Work out the size of each angle marked with a letter. Give reasons for your answers.

Problem 6 :

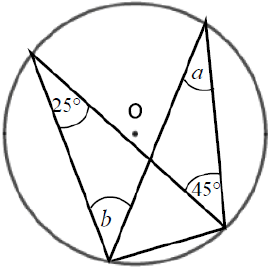
Solution :

a = 25 and b = 45

Because angles in the same arc.

Problem 7 :

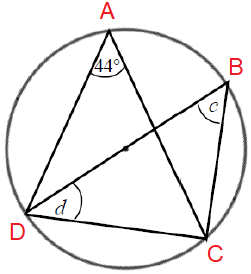
Solution :

c = 44 (angle in the same arc CD)

∠DCB = 90

In triangle DCB,

∠DCB + ∠CDB + ∠DBC = 180

90 + d + c = 180

90 + d + 44 = 180

134 + d = 180

d = 180 - 134

d = 46

Problem 8 :

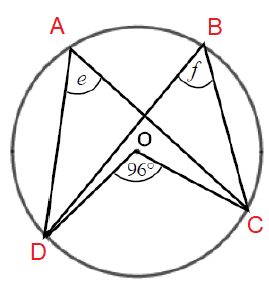
Solution :

∠DOC = 96

∠DOC = 2e

96 = 2e

e = 96 / 2

e = 48

f = 48

Angle in the same arc.

Problem 9 :

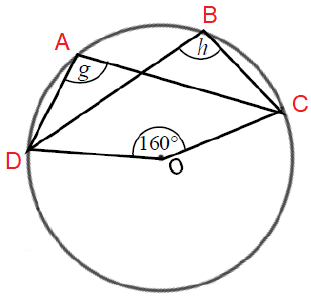
Solution :

Reflex of angle DOC = 360 - 160 ==> 200

Reflex of angle DOC ==> 2g = 200

g = 100

h = 100

Angle in the same arc.

Problem 10 :

D is the point on the circumference of the circle such that angle BDC = 60

i) Write down the size of angle CAB

ii) Work out the size of angle ACB.

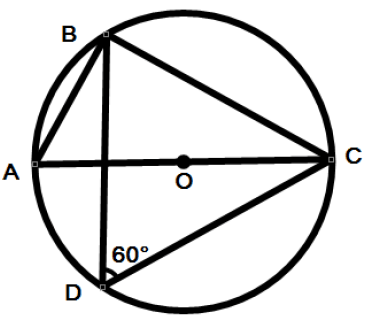
Solution :

∠BDC = 60, then ∠BAC = 60

In triangle ABC,

∠BAC + ∠ABC + ∠ACB = 180

60 + 90 + ∠ACB = 180

150 + ∠ACB = 180

∠ACB = 180 - 150

∠ACB = 30