ANGLE RELATIONSHIPS WITH PARALLEL LINES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
When two lines are parallel and they cut by the transversal, the following pairs will be congruent.
- Corresponding angles
- Alternate interior angles
- Alternate exterior angles
Sum of consecutive interior angles on the same side of the transversal will be equal to 180 degree.
Find the angle x in the figure given below. Give your reason.
Example 1 :
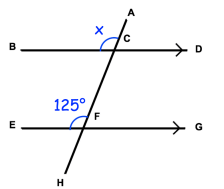
Solution :
<ACB and <AFE are corresponding angles, so they will be equal.
x = 125
Example 2 :
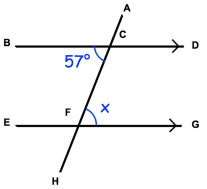
Solution :
<BCF = <GFC
Because they are alternate interior angles.
x = 57
Example 3 :
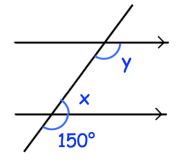
Solution :
Here x and 150 are linear pair, they add upto 180 degree.
150+ x = 180
x = 180-150
x = 30
x and y are consecutive interior angles on the same side of the transversal.
x+y = 180
30+ y = 180
y = 180 - 30
y = 150
Example 4 :
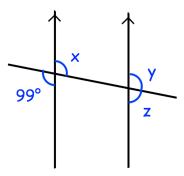
Solution :
The relationship between 99 and z :
They are corresponding angles.
So, z = 99
The relationship between z and y :
They are linear pair.
x + y = 180
99 + y = 180
y = 180 - 99
y = 81
The relationship between x and y :
They are corresponding angles.
x = y
x = 81
Example 5 :
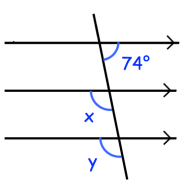
Solution :
x + 74 = 180
x = 180 - 74
x = 106
Relationship between x and y :
They are corresponding angles, so they are equal.
y = 106
Example 6 :
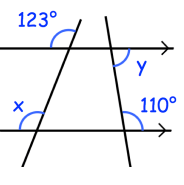
Solution :
Relationship between y and 110 :
They are consecutive interior angles on the same side of the transversal.
y + 110 = 180
y = 180 - 110
y = 70
Relationship between x and 123 :
They are corresponding angles.
x = 123
Example 7 :
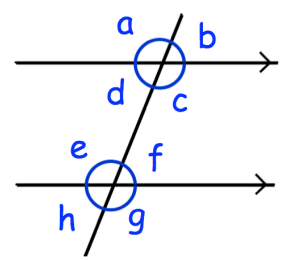
(a) Which angle is corresponding to angle c?
(b) Which angle is alternate to angle d?
(c) Which angle is corresponding to angle h?
(d) Which angle is vertically opposite to angle a?
(e) Which angle is alternate to angle e?
(f) Which angle is co-interior with angle c?
(g) Which angle is vertically opposite to angle h?
(h) Which angle is co-interior with angle e?
(i) Which angle is corresponding to angle a?
(j) Which angle is vertically opposite to angle g?
Solution :
(a) Corresponding angle of ∠c is ∠f.
(b) ∠d and ∠f are alternate angles.
(c) The corresponding angle of ∠h is ∠d.
(d) Vertically opposite to ∠a is ∠c.
(e) Alternate angle of ∠e is ∠c.
(f) The co-interior ∠c is ∠f.
(g) Vertically opposite to ∠h is ∠f.
(h) Co-interior angle with ∠e is ∠d.
(i) Corresponding to ∠a is ∠e.
(j) Vertically opposite to ∠g is ∠e.
Example 8 :
Find the value of the variable(s) in each figure.
Explain your reasoning.
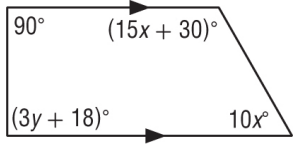
Solution :
Sum of co interior angles is 180.
15x+30 + 10x = 180 ----(1)
25x + 30 = 180
Subtract 30 on both sides.
25x = 180 - 30
25x = 150
Divide by 25 on both sides.
x = 150/25
x = 6
90 + 3y + 18 = 180 ------(2)
108 + 3y = 180
3y = 180 - 108
3y = 72
Divide by 3 on both sides.
y = 72/3
y = 24
Example 9 :
Find the value of the variable(s) in each figure. Explain
your reasoning.
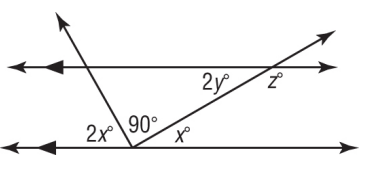
Solution :
Here 2x, 90 and x are linear pair. So, they add upto 180.
2x + 90 + x = 180
3x + 90 = 180
Subtract 90 on both sides.
3x = 180 - 90
3x = 90
Divide 3 on both sides.
x = 90/3
x = 30
2y and x are alternate interior angles.
2y = x
2y = 30
y = 30/2
y = 15
x and z are consecutive interior angles on the same side of the transversal.
x + z = 180
30 + z = 180
Subtract 30 on both sides.
z = 180 - 30
z = 150
Example 10 :
(Using a 3rd parallel Line – Auxilury Line)
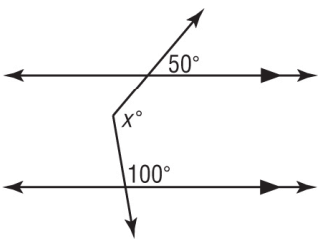
Solution :
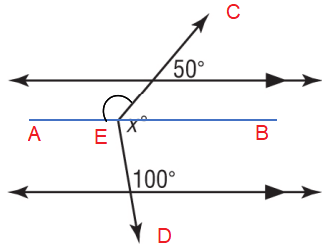
∠CEA = 130
Because its corresponding angle is 130 degree.
∠DEA = 100
Because alternate interior angles.
∠CEA + ∠DEA + x = 360
130 + 100 + x = 360
230 + x = 360
Subtract 230 on both sides.
x = 360 - 230
x = 130
Example 11 :
Use the figure to find the measures of the numbered angles. Explain your reasoning.
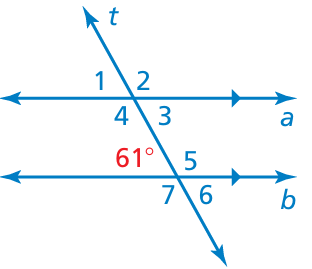
Solution :
∠1 and 61 are corresponding angles.
∠1 = 61
∠4 and 61 are co-interior angles. Then, their sum is 180 degree.
∠4 + 61 = 180
∠4 = 180 - 61
∠4 = 119
∠2 = ∠4 (vertical angles)
∠2 = 119
∠1 = ∠3 (vertical angles)
∠3 = 61
∠6 = 61 (Vertical angles)
∠4 = ∠7 (Corresponding angles)
∠7 = 119
∠5 = 119 (vertical angles)
Example 12 :
Use the figure to find the measures of the numbered angles. Explain your reasoning.
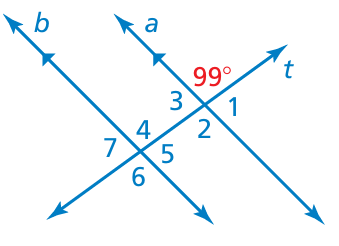
Solution :
∠1 + 99 = 180
∠1 = 180 - 99
∠1 = 81
∠3 = 81 (vertical angles)
∠1 = ∠5 = 81 (Corresponding angles)
∠2 = 99 (vertical angles)
∠2 = ∠6 = 99 (Corresponding angles)
∠7 = 81
∠4 = 99 (Corresponding angles)
Example 13 :
Use the figure to find the measures of the numbered angles. Explain your reasoning.
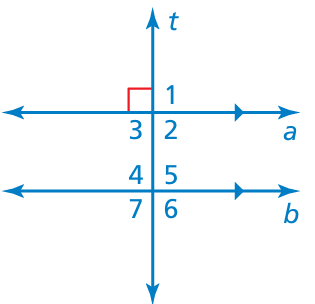
Solution :
The shown angle measures is 90 degree.
∠1 = 90
∠2 = 90 (vertical angles)
∠3 = 90 (corresponding angles)
∠4 = ∠5 = ∠6 = ∠7 = 90 degree
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling