ANGLE BISECTOR THEOREM WORKSHEET

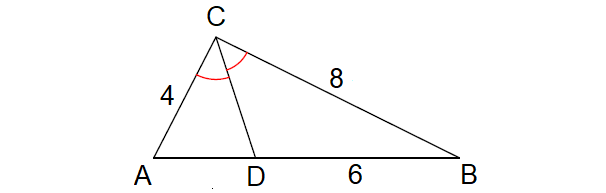
1. In the ΔABC shown below, find the length of AD.

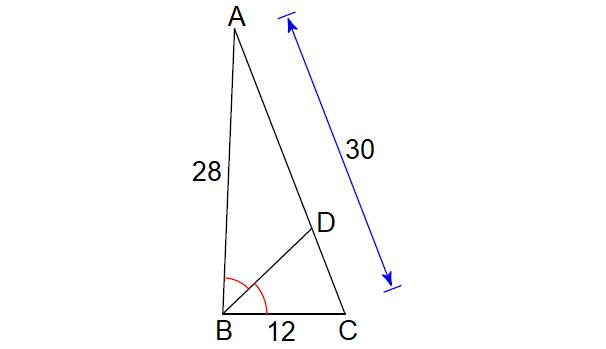
2. In the ΔABC shown below, find the length of CD.

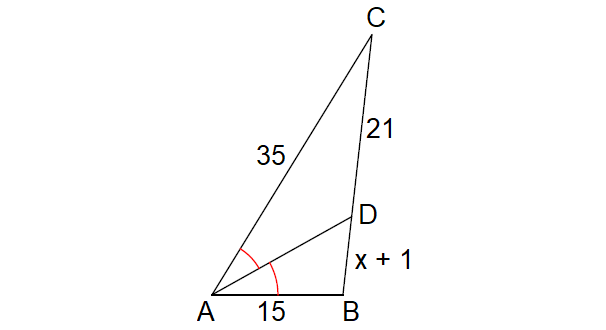
3. Solve for x.

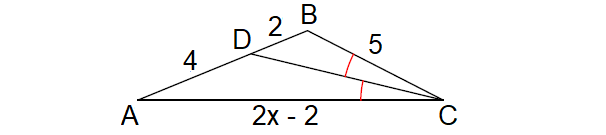
4. Solve for x.

5. Solve for x.

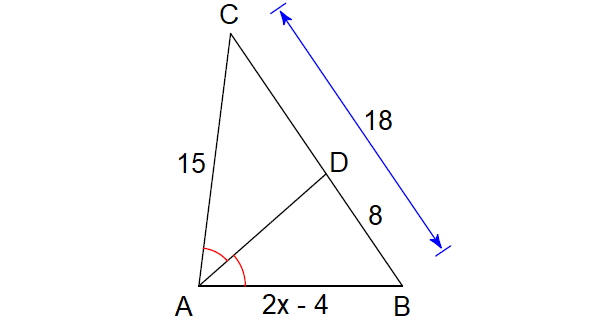
6. Solve for x.

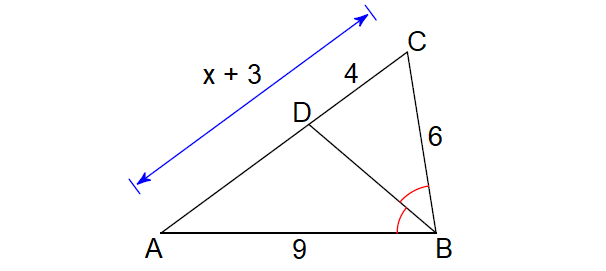
Answers

1. Answer :

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

AD/DB = CA/CB

Substitute.

AD/6 = 4/8

AD/6 = 1/2

Multiply both sides by 6.

AD = 3

2. Answer :

Let x be the length of CD.

Find the length of  DA :

DA = CA - CD

= 30 - x

Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Substitute.

x/(30 - x) = 12/28

x/(30 - x) = 3/7

7x = 3(30 - x)

7x = 90 - 3x

Add 3x to both sides.

10x = 90

Divide both sides by 10.

x = 9

CD = 9

3. Answer :

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

BD/DC = AB/AC

Substitute.

(x + 1)/21 = 15/35

(x + 1)/21 = 3/7

7(x + 1) = 3(21)

7x + 7 = 63

Subtract 7 from both sides.

7x = 56

Divide both sides by 7.

x = 8

4. Answer :

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

BD/DA = CB/CA

Substitute.

2/4 = 5/(2x - 2)

1/2 = 5/(2x - 2)

1(2x - 2) = 5(2)

2x - 2 = 10

Add 2 to both sides.

2x = 12

Divide both sides by 2.

x = 6

5. Answer :

Find the length of DC :

DC = BC - DC

= 18 - 8

= 10

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

BD/DC = AB/AC

Substitute.

8/10 = (2x - 4)/15

4/5 = (2x - 4)/15

15(4) = 5(2x - 4)

60 = 10x - 20

Add 20 to both sides.

80 = 10x

Divide both sides by 10.

8 = x

6. Answer :

Find the length of DA :

DA = CA - CD

= (x + 3) - 4

= x + 3 - 4

= x - 1

Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Substitute.

4/(x - 1) = 6/9

4/(x - 1) = 2/3

3(4) = 2(x - 1)

12 = 2x - 2

Add 2 to both sides.

14 = 2x

Divide both sides by 2.

7 = x