ANGLE BISECTOR OF A TRIAGLE THEOREM

If a point is on the bisector of an angle, then it is equidistant from the sides of the angle.

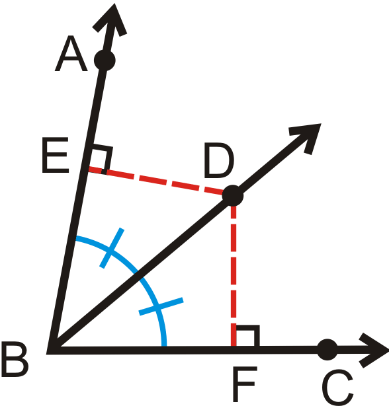
BD bisects ∠ABC

DE and DF are perpendiculars for AB and AC respectively.

∠EBD = ∠FBD

∠DEB = ∠DFB

BD = BD (Common)

Then, triangles BED and BDF are congruent.

ED = DF

BE = BF

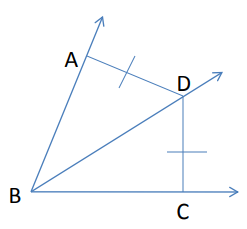
Problem 1 :

If BD bisects the angle ∠ABC

m∠ABD = 4x - 10 and m∠CBD = 7x - 31, find ∠CBD.

Solution :

∠ABD = ∠DBC

4x - 10 = 7x - 31

4x - 7x = -31 + 10

-3x = -21

Dividing by -3 on both sides,

x = 7

Applying the value of x in ∠DBC

∠DBC = 7x - 31

= 7(7) - 31

= 49 - 31

∠DBC = 18

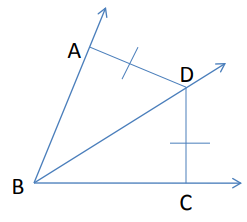
Problem 2 :

If BD bisects the angle ∠ABC,

m∠ABD = 3x + 15 and m∠CBD = 4x + 4, find m∠ ABC.

Solution :

∠ABD = ∠DBC

3x + 15 = 4x + 4

3x - 4x = 4 - 15

-x = -11

x = 11

m∠ ABC = ∠DBC + ∠ABD

= 4x + 4 + 3x + 15

= 7x + 19

= 7(11) + 19

= 77 + 19

m∠ABC = 96

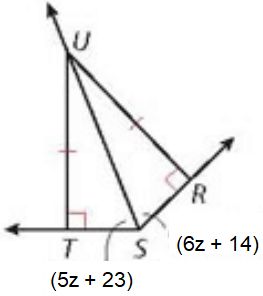
Problem 3 :

Find m∠TSU

Solution :

In triangles TSU and USR.

∠UTS = ∠URS

UT = UR

US = US (Common)

∠UST = ∠USR (By CPCTC)

5z + 23 = 6z + 14

5z - 6z = 14 - 23

-z = -9

z = 9

∠TSU = 5z + 23

= 5(9) + 23

∠TSU = 68

Problem 4 :

Given that 𝑚∠𝑊𝑌𝑍 = 63, XW = 5.7, and ZW = 5.7, then 𝑚∠𝑋𝑌𝑍 = _____________.

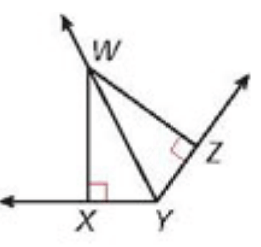
Solution :

Using angle bisector theorem of triangle.

𝑚∠𝑊𝑌𝑍 = 63

𝑚∠XYZ = 2(63) => 126

Problem 5 :

Find 𝑚∠QRS

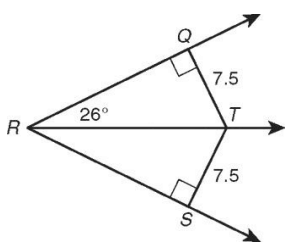
Solution :

∠QRT = ∠SRT

∠QRS = 2(26)

∠QRS = 52

Problem 6 :

Find ∠WXZ

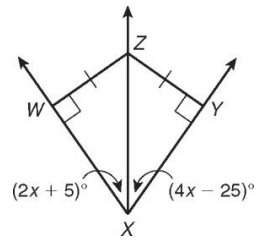
Solution :

∠WXZ = ∠ZXY

2x + 5 = 4x - 25

2x - 4x = -25 - 5

-2x = -30

x = 15

Applying the value of x.

∠WXZ = 2x + 5

∠WXZ = 2(15) + 5

∠WXZ = 35

Problem 7 :

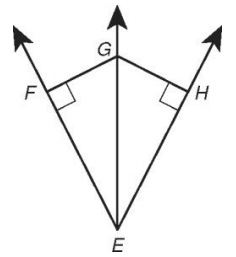
(i) Given that FG = HG and m∠FEH = 56, find m∠GEH. 

(ii)  Given that EG bisects ∠FEH and GF = √2, find GH.

Solution :

i)  m∠FEH = 56 =  m∠GEH

(ii) Since EG bisects ∠FEH, GF and GH are congruent.

If GF = √2 then GH = √2

Problem 8 :

EG is angle bisector.

(i) Given that ∠FEG ≅ ∠GEH, FG = HG and FG = 10z – 30, HG = 7z + 6 then find GF.

(ii) Given that GF = GH, m∠GEF = 8a , and m∠GEH = 24, find a

Solution :

Accordingly angle bisector theorem,

FG = 10z – 30 ----(1) HG = 7z + 6 ----(2)

(1) = (2)

10z -  30 = 7z + 6

10z - 7z = 6 + 30

3z = 36

z = 36/3

z = 12

Applying the value of FG = 10z - 30

= 10(12) - 30

= 120 - 30

FG = 90

(ii)  m∠GEF = 8a ---(1)  m∠GEH = 24 ----(2)

(1) = (2)

8a = 24

a = 24/8

a = 3