ANGLE BISECTOR AND SUPPLEMENTARY ANGLES

Angle bisector :

An angle bisector is defined as a ray, segment, or line that divides a given angle into two angles of equal measures. The word bisector or bisection means dividing into equal parts.

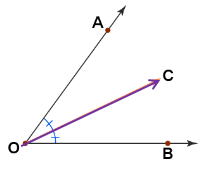
∠AOC and ∠COB are equal.

Supplementary angles :

Two angles are supplementary angles if the sum of their measures is equal to 180 degrees.

Problem 1 :

Which angles are named in the pictures below.

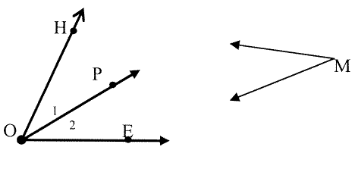
Solution:

When an angle measures between 0° and 90°. It is called an acute angle.

The acute angles are ∠HOP and ∠POE.

Problem 2 :

If m ∡ABD = 22° and m ∡DBC = 53°, then find m ∡ABC.

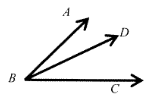
Solution:

∡ABC = ∡ABD + ∡DBC

∡ABC = 22° + 53°

∡ABC = 75°

Problem 3 :

Find m ∠1 and m ∠2

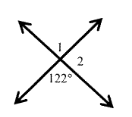
Solution:

∠1 = 122° (vertically opposite angles)

122° + ∠2 = 180° (linear pair)

∠2 = 180 - 122

∠2 = 58°

Problem 4 :

Find m∠ABC if BD is an angle bisector.

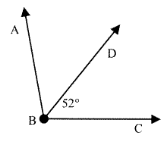
Solution:

m∠ABC = 2 × ∠DBC

= 2 × 52°

m∠ABC = 104°

Problem 5 :

Find m ∠ABC if BD is an angle bisector.

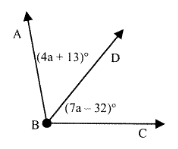
Solution:

∠ABD = ∠DBC

4a + 13 = 7a - 32

7a - 4a = 32 + 13

3a = 45

a = 15

m ∠ABC = 2 × ((4 × 15) + 3)°

= 2 × 73°

m ∠ABC = 146°

Problem 6 :

If m∠1 = (2x + 45)° and m∠2 = (5x - 45)°, find m∠1.

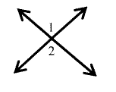
Solution:

m∠1 = m∠2 (vertically opposite angles)

2x + 45 = 5x - 45

5x - 2x = 45 + 45

3x = 90

x = 30

m∠1 = (2x + 45)°

= (60 + 45)°

m∠1 = 105°

Problem 7 :

What is the supplement of a 56° angle?

Solution:

Supplement of the angle = 180° - x

= 180° - 56°

= 124°

Problem 8 :

If ∡A and ∡B are supplementary, and m ∡A = (7x + 16)°, and m ∡B = (9x - 12)°. Write the equation you would use to find x.

Solution:

The sum of the measures of two supplementary angles is 180°.

m ∡A + m ∡B = 180°

7x + 16 + 9x - 12 = 180°

16x + 4 = 180°

16x = 176

x = 11