ANALYZE THE EQUATION OF A PARABOLA
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
The parabola will be in four different forms,
|
(y - k)2 = 4a(x - h) |
Opening right |
|
(y - k)2 = -4a(x - h) |
Opening left |
|
(x - h)2 = 4a(y - k) |
Opening up |
|
(x - h)2 = -4a(y - k) |
Opening down |
Write the following in standard form. Identify the
- Vertex
- Focus
- Axis of symmetry
- Direction of opening of parabola.
- Equation latus rectum and directrix
- Draw the graph
Problem 1 :
y = 3x2 + 24x + 50
Solution :
y = 3x2 + 24x + 50
y = 3[x2 + 8x] + 50
= 3[x2 + 2x(4) + 42 - 42] + 50
= 3[(x + 4)2 - 42] + 50
= 3[(x + 4)2 - 16] + 50
= 3(x + 4)2 - 48 + 50
y = 3(x + 4)2 + 2
y - 2 = 3(x + 4)2
Comparing with
(y - k) = 4a(x - h)2
The parabola is symmetric about y-axis and open upward.
4a = 3
a = 3/4
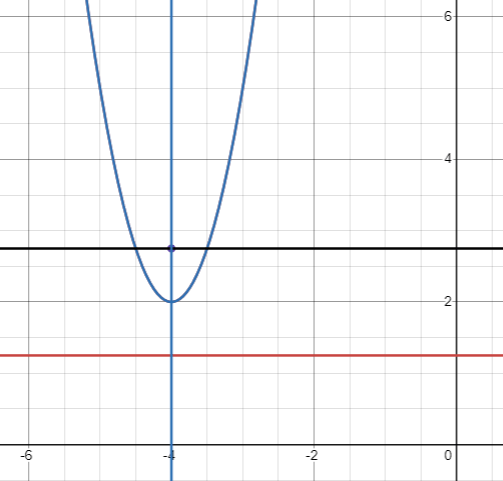
|
Vertex |
(h, k) ==> (-4, 2) |
|
Focus |
(h, k + a) k + a = 2 + (3/4) = 11/4 (-4, 11/4) |
|
Equation of latus rectum |
y = k + a y = 11/4 |
|
Equation of directrix |
y = k - a y = 2 - (3/4) y = 5/4 |
|
Axis of symmetry |
x = -4 |
|
Equation of directrix |
4a = 3 units |
Problem 2 :
-6y = x2
Solution :
x2 = -6y
The parabola is symmetric about y-axis and open downward.
4a = 6
a = 6/4
a = 3/2
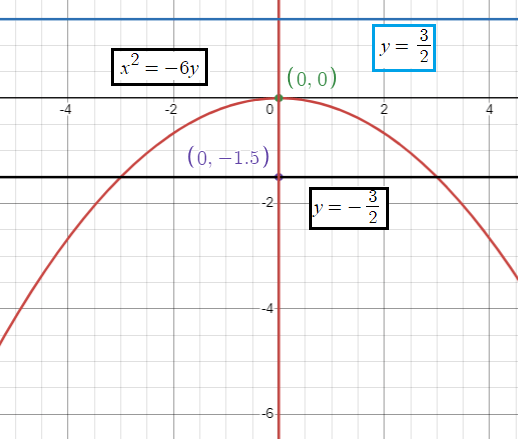
|
Vertex |
(h, k) ==> (0, 0) |
|
Focus |
(0, -a) (0,-3/2) |
|
Equation of latus rectum |
y = -a y = -3/2 |
|
Equation of directrix |
y = a y = 3/2 |
|
Axis of symmetry |
x = 0 |
|
Equation of directrix |
4a = 6 units |
Problem 3 :
3(y - 3) = (x - 6)2
Solution :
(x - 6)2 = 3(y - 3)
(x - h)2 = 4a(y - k)
The parabola is symmetric about y-axis and open upward.
4a = 3
a = 3/4
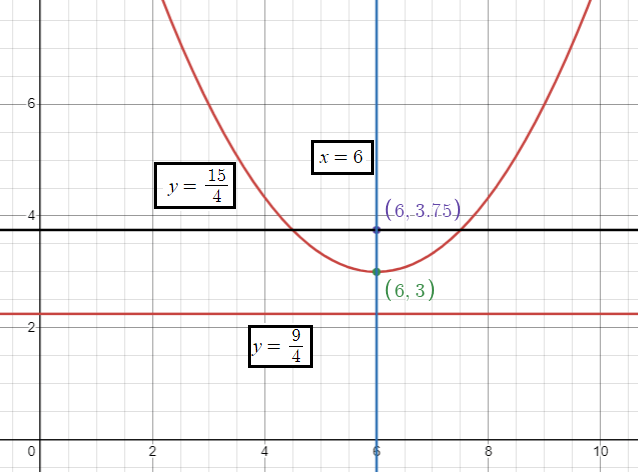
|
Vertex |
(h, k) ==> (6, 3) |
|
Focus |
(h, k + a) k + a = 3 + (3/4) = 15/4 (6, 15/4) |
|
Equation of latus rectum |
y = k + a y = 15/4 |
|
Equation of directrix |
y = k - a y = 3 - (3/4) y = 9/4 |
|
Axis of symmetry |
x = 6 |
|
Equation of directrix |
4a = 6 units |
Problem 4 :
-2(y - 4) = (x - 1)2
Solution :
(x - 1)2 = -2(y - 4)
(x - h)2 = -4a(y - k)
The parabola is symmetric about y-axis and open downward.
4a = 2
a = 2/4
a = 1/2
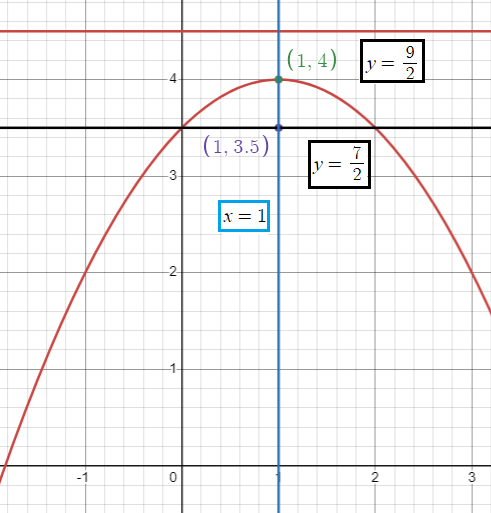
|
Vertex |
(h, k) ==> (1, 4) |
|
Focus |
(h, k - a) k - a = 4 - (1/2) = 7/2 (1, 7/2) |
|
Equation of latus rectum |
y = k - a y = 7/2 |
|
Equation of directrix |
y = k + a y = 4 + (1/2) y = 9/2 |
|
Axis of symmetry |
x = h x = 1 |
|
Equation of directrix |
4a = 2 units |
Problem 5 :
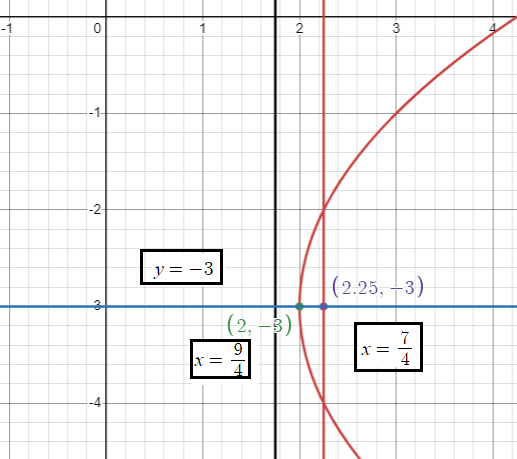
4(x - 2) = (y + 3)2
Solution :
4(x - 2) = (y + 3)2
(x - h)2 = 4a(y - k)
The parabola is symmetric about x-axis and open rightward.
4a = 1
a = 1/4
|
Vertex |
(h, k) ==> (2, -3) |
|
Focus |
(h + a, k) h + a = 2 + (1/4) = 9/4 (9/4, -3) |
|
Equation of latus rectum |
x = h + a x = 9/4 |
|
Equation of directrix |
x = h - a x = 2 - (1/4) x = 7/4 |
|
Axis of symmetry |
y = k y = -3 |
|
Equation of directrix |
4a = 1 unit |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling