ALTERNATE LIMIT DEFINITION OF DERIVATIVE

Problem 1 :

The alternate definition of the derivative at the point x = a is

use the alternate definition to find f'(4) if f(x) = 8x - 7

Solution :

f(x) = 8x - 7

Here a = 4

f(4) = 8(4) - 7

= 32 - 7

= 25

Problem 2 :

Use the alternate definition to find f'(1) if f(x) = x³

Solution :

f(x) = x³

f(a) = a³

Here a = 1, then f(1) = 1³ => 1

Problem 3 :

Use the alternate definition to find h'(2), where

h(x) = x³ + x² - x

Solution :

h(x) = x³ + x² - x

Here a = 2

h(2) = 2³ + 2² - 2

= 8 + 4 - 2

= 12 - 2

h(2) = 10

h(x) - h(2) = x³ + x² - x - 10

Using synthetic division, factoring the numerator.

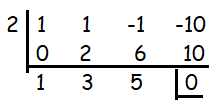
(x - 2)(x² + 3x + 5)

Problem 4 :

Use the alternate definition to find f'(6), where

f(x) = 9x + 18

Solution :

f(x) = 9x + 18

Here x = 6

f(6) = 9(6) + 18

= 54 + 18

f(6) = 72

Problem 5 :

Use the alternate definition to find f'(-5), where

f(x) = -2x² + 4x + 1

Solution :

f(x) = -2x² + 4x + 1

Here a = -5

f(-5) = -2(-5)² + 4(-5) + 1

= -2(25) - 20 + 1

= -50 - 20 + 1

f(-5) = -69

Applying x = -5, we get

= -2(-5-7)

= -2(-12)

= 24

Problem 6 :

Use the alternate limit definition to find g'(-2), if 

g(x) = 6x² - 8x + 3

Solution :

g(x) = 6x² - 8x + 3

Here a = -2

f(-2) =  6(-2)² - 8(-2) + 3

= 6(4) + 16 + 3

= 24 + 16 + 3

= 43