ALGEBRA PRACTICE QUESTIONS WITH SOLUTIONS

Problem 1 :

The graph of quadratic function r is shown on the grid.

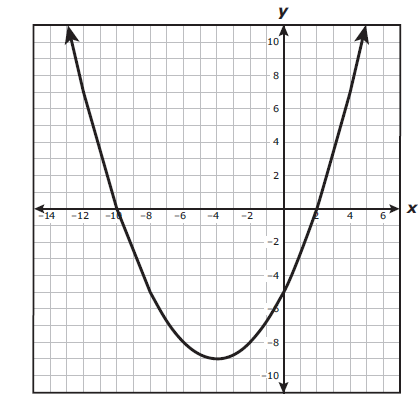
Which answer choice best represents the intercepts of the graph of r ?

Solution :

By observing the figure, 

x -intercepts are (-10, 0) and (2, 0) while the y - intercepts are (0, -5)

So, option D) is correct.

Problem 2 :

A worker is packing items in boxes. The table shows the linear relationship between the number of items the worker has packet in boxes after different amounts of time.

Items Packed in Boxes

Which statement describes the rate of change of the number of items the worker packed in boxes with respect to the number of minutes the worker has been packing items in boxes ?

F) The worker packed 8 items in boxes per minute.

G) The worker packed 37 items in boxes per minute.

H) The worker packed 4 items in boxes per minute.

J) The worker packed 15 items in boxes per minute.

Solution :

rate of change = Δy/Δx

= (28 - 20)/(7 - 5)

= 8/2

= 4

Hence, the worker packed 4 items in boxes per minute.

So, option C) is correct.

Problem 3 :

A system of equations is graphed on the grid.

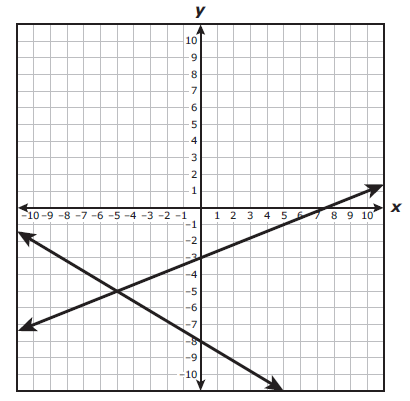
Which system of equations is best represented by the graph ?

Solution :

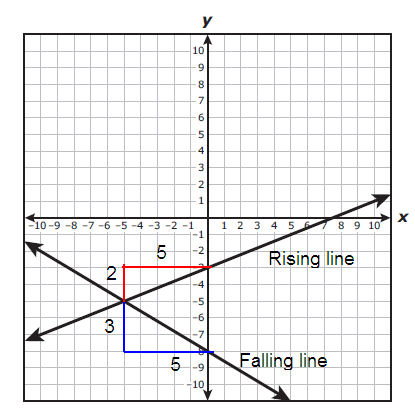
y = mx + b

Rising line :

Slope (m) = 2/5

y intercept = -3

y = (2/5)x - 3

Falling line :

Slope (m) = -3/5

y - intercept = -8

y = -(3/5)x - 8

So, option (B) is correct.

Problem 4 :

Which graph represents y as a function of x ?

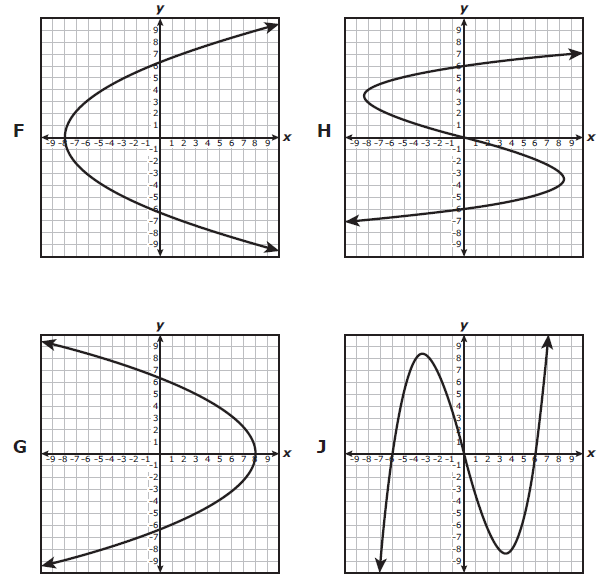
Solution :

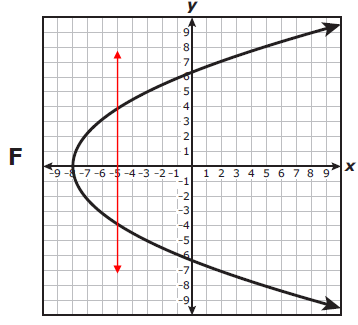The given graph intersects the vertical line at three points. Hence, it is not a function.

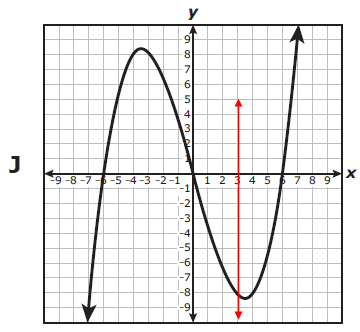The given graph intersects the vertical line at one point. So, it is a function.

Problem 5 :

What is the solution to this system of equations ?

2x + y = 40

x – 2y = -20

A) (12, 16)     B)(15, 17.5)    C) There is no solution.

D) There are an infinite number of solutions.

Solution :

Given, 2x + y = 40 --- (1)

y = 40 - 2x --- (2)

x – 2y = -20 --- (3)

y = 40 - 2x substitute in equation (3).

x - 2(40 - 2x) = -20

x - 80 + 4x = -20

-80 + 5x = -20

5x = -20 + 80

5x = 60

x = 60/5

x = 12

x = 12 substitute the equation (2).

y = 40 - 2(12)

y = 40 - 24

y = 16

So, option A) is correct.

Problem 6 :

Which graph best represents a quadratic function with a range of all real numbers greater than or equal to 3 ?

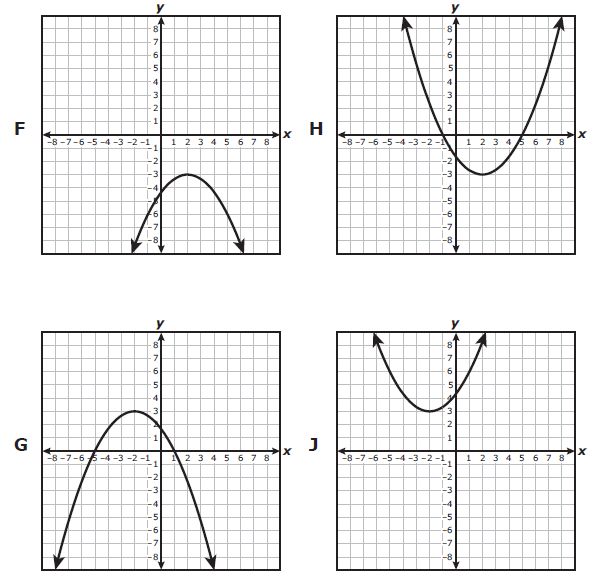
Problem 7 :

The value of y is directly proportional to the value of x. When x = 512, y = 128.

What is the value of y when x = 64 ?

A) 256     B) 32    C) 16    D)  8

Solution :

Given, the value of y is directly proportional to the value of x.

y = kx

128 = k(512)

128/512 = k

k = 1/4

y = x/4

y = 64/4

y = 16

So, option C) is correct.

Problem 8 :

A customer is buying bath towels and hand towels and can spend no more than $100. Each bath towel costs $8, and each hand towel costs $5. The inequality 8x + 5y ≤ 100 represents all possible combinations of x, the number of bath towels, and y, the number of  hand towels the customer can buy.

Which graph best represents the solution set for this inequality ?

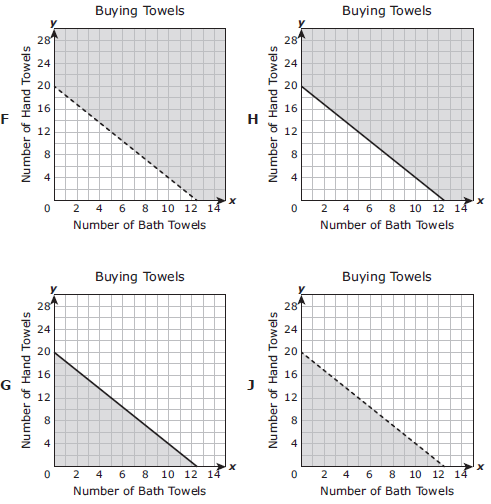
Solution :

Since the inequality sign involved here is less than or equal. So, we ignore F and J.

Option G is correct.

Problem 9 :

An exponential function is graphed on the grid.

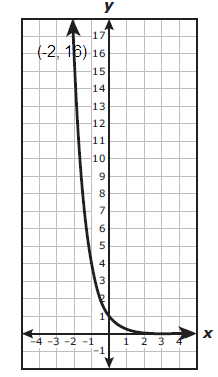
Which function is best represented by the graph ?

A) p(x) = (0.25)^x         B) p(x) = 2(0.5)^x

C) p(x) = (1.25)^x         D) p(x) = (25)^x

Solution :

The exponential function will be in the form,

y = ab^x

Choosing two points from the graph,

(-1, 4) and (-2, 16)

Applying the point (-1, 4), we get

4 = ab^-1

4 = a/b

4b = a----(1)

Applying the point (-2, 16), we get

16 = ab^-2

16 = a/b^{2 ----(2)}

Applying the value of a, we get

16 = 4b/b²

1/b = 4

b = 1/4

a = 4(1/4)

a = 1

Applying the value of a and b, we get

y = (0.25)^x

So, option A is correct.

Problem 10 :

Which expression is equivalent to (n - 4) (2n + 7) ?

F) 3n + 3    G) n - 28     H) 2n² -15n - 28    J)  2n² - n - 28

Solution :

Given, (n - 4) (2n + 7)

2n² + 7n - 8n - 28

2n² - n - 28

Hence, option J) is correct.

Problem 11 :

Which situation shows causation ?

A)  When the number of people in a bus increases, the number of animals in a zoo also increases.

B) When the number of hours worked each week by an hourly employee decreases, the amount of money earned by the employee also decreases.

C) When the amount of a discount for a sale increases, the number of items sold during the sale decreases.

D) When the number of bike trails in a city decreases, the amount of rainfall in the city increases. 

Solution :

Just like 

Hence, option B is correct.

More work, more gain, the less you pay, the less you get.

Problem 12 :

A system of linear equations is represented by line h and line j, A table representing some points on line h and the graph of line j are shown.

Line h

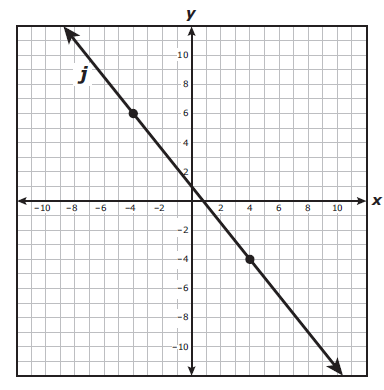
Which system of equations is best represented by lines h and j ?

Solution :

Choosing two points from the table,

Let (x₁, y₁) = (-16, 7) and (x₂, y₂) = (-8, 1)

Slope (m) = (1 - 7)/(-8 + 16)

= -6/8

= -3/4

Equation of the line h :

Slope (m) = -3/4 and point (-8, 1)

y - 1 = (-3/4)(x + 8)

4(y - 1) = -3(x + 8)

4y - 4 = -3x - 24

4y = -3x - 20

y = (-3/4) x - 5

To find equation of a line J :

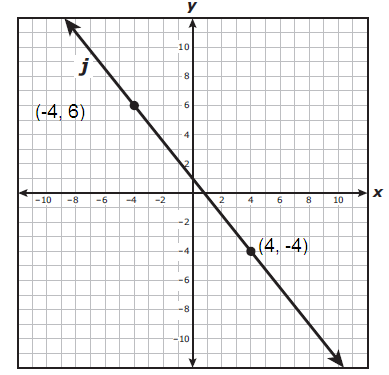
It passes through the point (-4, 6) and (4, -4).

Let (x₁, y₁) = (-4, 6)

(x₂, y₂) = (4, -4)

m = (-4 - 6)/(4 + 4)

m = -10/8

m = -5/4

Equation of line J :

(y + 4) = (-5/4)(x - 4)

4(y + 4) = -5(x - 4)

4y + 16 = -5x + 20

4y = -5x + 4

y = (-5/4)x + 1

So, option j is correct.