ADDING SUBTRACTING MULTIPLYING AND DIVIDING FUNCTIONS FROM GRAPH

To add, subtract, multiply or divide two functions from graph, we have to perform the same arithmetic operation with the outputs of the function f(x) and g(x). Let us see this briefly.

Let the given functions as f(x) and g(x).

Adding functions :

(f + g)(x) = f(x) + g(x)

Let (x, a) and (x, b) be the coordinates in the function f(x) and g(x) respectively. To add these two functions, we follow the rule following.

(f + g)(x) ==> (x, a + b)

Subtracting functions :

(f - g)(x) = f(x) - g(x)

Let (x, a) and (x, b) be the coordinates in the function f(x) and g(x) respectively. To subtract these two functions, we follow the rule following.

(f - g)(x) ==> (x, a - b)

Multiplying functions :

(f ⋅ g)(x) = f(x) ⋅ g(x)

Let (x, a) and (x, b) be the coordinates in the function f(x) and g(x) respectively. To multiply these two functions, we follow the rule following.

(f ⋅ g)(x) ==> (x, a ⋅ b)

Dividing functions :

(f / g)(x) = f(x) / g(x)

Let (x, a) and (x, b) be the coordinates in the function f(x) and g(x) respectively. To multiply these two functions, we follow the rule following.

(f / g)(x) ==> (x, a / b)

Use the graphs of f and g to evaluate the functions.

add-sub-mul-div-function-q1

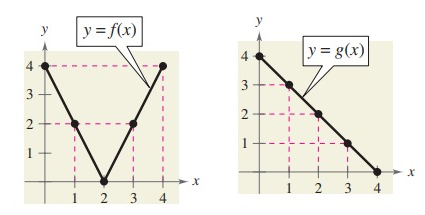
Problem 1 :

a) (f + g)(3)       b) (f/g)(2)

Solution:

(f + g)(3) = f(3) + g(3)

= 2 + 1

(f + g)(3) = 3

b) (f/g)(2)

Solution:

(f/g)(2) = f(2)/g(2)

= 0/2

(f/g)(2) = 0

Problem 2 :

a) (f - g)(1)         b) (fg)(4)

Solution:

(f - g)(1) = f(1) - g(1)

= 2 - 3

(f - g)(1) = -1

b) (fg)(4)

Solution:

(fg)(4) = f(4) ⋅ g(4)

= 4 ⋅ 0

(fg)(4) = 0

Problem 3 :

a) (f ∘ g)(2)            b) (g ∘ f)(2)

Solution:

(f ∘ g)(2) = f[g(2)]

= f(2)

(f ∘ g)(2) = 0

b) (g ∘ f)(2)

Solution:

(g ∘ f)(2) = g[f(2)]

= g(0)

(g ∘ f)(2) = 4

Problem 4 :

a) (f ∘ g)(1)        b) (g ∘ f)(3)

Solution:

(f ∘ g)(1) = f[g(1)]

= f(3)

(f ∘ g)(1) = 2

b) (g ∘ f)(3)

Solution:

(g ∘ f)(3) = g[f(3)]

= g(2)

(g ∘ f)(3) = 2

Use the graphs of f and g to solve. 

add-sub-mul-div-function-q2.png

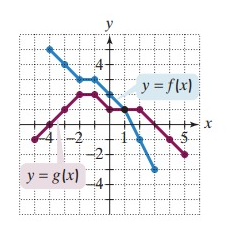
Problem 5 :

Find (f + g)(-3)

Solution:

(f + g)(-3) = f(-3) + g(-3)

= 4 + 1

= 5

Problem 6 :

Find (g - f)(-2).

Solution:

(g - f)(-2) = g(-2) - f(-2)

= 2 - 3

= -1

Problem 7 :

Find (fg)(2)

Solution:

(fg)(2) = f(2) ⋅ g(2)

= -1 ⋅ 1

= -1

Problem 8 :

Find (g/f)(3)

Solution:

(g/f)(3) = g(3)/f(3)

= 0/-3

= 0

Problem 9 :

Draw the graph of of f + g and find domain and range.

Solution:

adding-sub-mul-dividing-with-fungraphq1

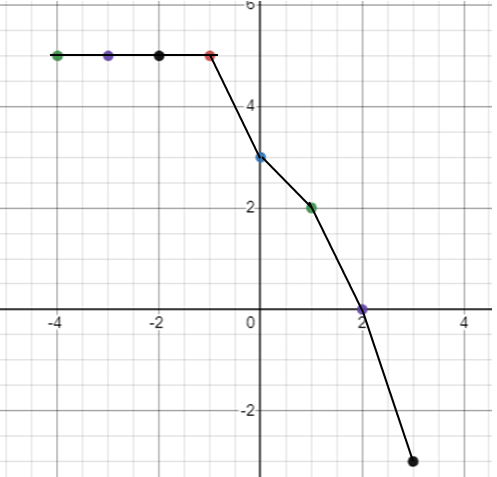
So, the domain of (f + g) is (-4, 3).

Problem 10 :

Find the domain of f/g.

Solution:

x

-5

-4

-3

-2

-1

0

1

2

3

4

5

f(x)

undefined

5

4

3

2

2

1

-1

-3

undefined

undefined

g(x)

-1

0

1

2

2

1

1

1

0

-1

-2

f/g

undefined

undefined

4

1.5

1.5

2

1

-1

undefined

undefined

undefined

So, the domain of (f/g) is (-3, 2).

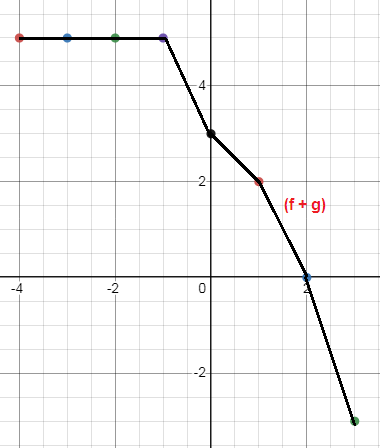
Problem 11 :

Graph f + g.

Solution:

x

-5

-4

-3

-2

-1

0

1

2

3

4

5

f(x)

undefined

5

4

3

2

2

1

-1

-3

undefined

undefined

g(x)

-1

0

1

2

2

1

1

1

0

-1

-2

f+g

undefined

5

5

5

4

3

2

0

-3

undefined

undefined

add-sub-mul-div-function-q9.png

Problem 12 :

Graph f - g.

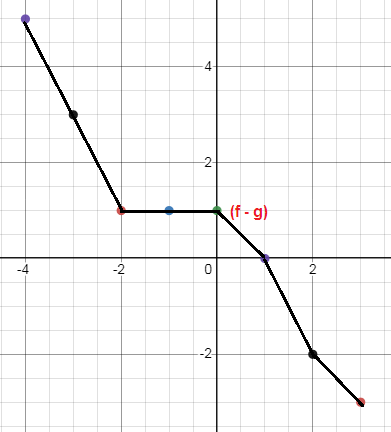
Solution:

x

-5

-4

-3

-2

-1

0

1

2

3

4

5

f(x)

undefined

5

4

3

2

2

1

-1

-3

undefined

undefined

g(x)

-1

0

1

2

2

1

1

1

0

-1

-2

f-g

undefined

5

3

1

0

1

0

-2

-3

undefined

undefined

add-sub-mul-div-function-q10.png

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More