ABSOLUTE VALUE EQUATIONS WITH TWO ABSOLUTE VALUES

When we solve absolute value functions with two absolute signs, we follow the rules given below.

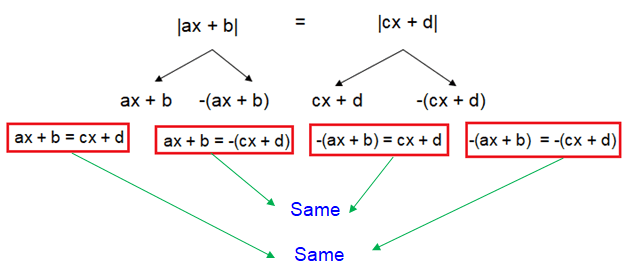
More simply,

|u| = |v|

u = v and -u = v

Solve the following absolute value equations.

Problem 1 :

|x + 4| = |2x - 7|

Solution :

 |x + 4| = |2x - 7|

x + 4 = 2x - 7

x - 2x = -7 - 4

-x = - 11

x = 11

x + 4 = - (2x - 7)

x + 4 = -2x + 7

x + 2x = 7 - 4

3x = 3

x = 1

So, the solution is x = 1 or x = 11.

Problem 2 :

|3x + 5| = |x - 6|

Solution :

|3x + 5| = |x - 6|

3x + 5 = x - 6

3x - x = -6 - 5

2x = -11

x = -11/2

3x + 5 = -(x - 6)

3x + 5 = -x + 6

3x + x = 6 - 5

4x = 1

x = 1/4

So, the solution is x = -11/2 or x = 1/4.

Problem 3 :

|x - 9| = |x + 6|

Solution :

|x - 9| = |x + 6|

x - 9 = x + 6

x - x = 6 - 9

0 = -3

it is not true.

|x - 9| = |x + 6|

x - 9 = - (x + 6)

x - 9 = -x - 6

x + x = -6 + 9

2x = 3

x = 3/2

So, the solution is 3/2.

Problem 4:

|x + 4| = |x - 3|

Solution :

|x + 4| = |x - 3|

x + 4 = x - 3

x - x = -3 - 4

0 = -7

it is not true.

|x + 4| = |x - 3|

x + 4 = -(x - 3)

x + 4 = -x + 3

x + x = 3 - 4

2x = -1

x = -1/2

So, the solution is -1/2.

Problem 5 :

|5t + 7| = |4t + 3|

Solution :

|5t + 7| = |4t + 3|

5t + 7 = 4t + 3

5t - 4t = 3 - 7

t = -4

|5t + 7| = |4t + 3|

5t + 7 = - (4t + 3)

5t + 7 = -4t - 3

5t + 4t = -3 - 7

9t = -10

t = -10/9

o, the solution is t = -4 or t = -10/9.

Problem 6 :

|3a - 1| = |2a + 4|

Solution :

|3a - 1| = |2a + 4|

3a - 1 = 2a + 4

3a - 2a = 4 + 1

a = 5

|3a - 1| = |2a + 4|

3a - 1 = - (2a + 4)

3a - 1 = -2a - 4

3a + 2a = -4 + 1

5a = -3

a = -3/5

So, the solution is a = 5 or a = -3/5.

Problem 7 :

|n - 3| = |3 - n|

Solution :

|n - 3| = |3 - n|

True for all real values of n. So, infinitely many solution.

Problem 8 :

|y - 2| = |2 - y|

Solution :

|y - 2| = |2 - y|

True for all real values of y. So, infinitely many solution.

Problem 9 :

|7 - a| = |a + 5|

Solution :

|7 - a| = |a + 5|

7 - a = a + 5

-a - a = 5 - 7

-2a = -2

a = 1

|7 - a| = |a + 5|

7 - a = - (a + 5)

7 - a = -a - 5

-a + a = -5 - 7

0 = -12

So, the solution is a = 1.

Problem 10 :

|6 - t| = |t + 7|

Solution :

|6 - t| = |t + 7|

6 - t = t + 7

-t - t = 7 - 6

-2t = 1

t = -1/2

|6 - t| = |t + 7|

6 - t = - (t + 7)

6 - t = -t - 7

-t + t = -7 - 6

0 = -13

So, the solution is t = -1/2.

Problem 11 :

|1/2x - 5| = |1/4x + 3|

Solution :

|1/2x - 5| = |1/4x + 3|

1/2x - 5 = 1/4x + 3

1/2x - 1/4x = 3 + 5

(2x - x)/4 = 8

x/4 = 8

x = 32

|1/2x - 5| = |1/4x + 3|

1/2x - 5 = - (1/4x + 3)

1/2x - 5 = -1/4x - 3

1/2x + 1/4x = -3 + 5

(2x + x)/4 = 2

3x/4 = 2

3x = 8

x = 8/3

So, the solution is x = 32 or x = 8/3.

Recent Articles

RSS

  1. Finding Range of Values Inequality Problems

    May 21, 24 08:51 PM

    Finding Range of Values Inequality Problems

    Read More

  2. Solving Two Step Inequality Word Problems

    May 21, 24 08:51 AM

    Solving Two Step Inequality Word Problems

    Read More

  3. Exponential Function Context and Data Modeling

    May 20, 24 10:45 PM

    Exponential Function Context and Data Modeling

    Read More