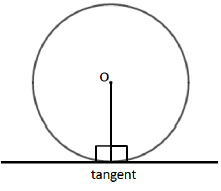
A LINE DRAWN FROM CENTER OF CIRCLE TO THE TANGENT LINE

Work out the size of each angle marked with a letter. Give reasons for your answers.

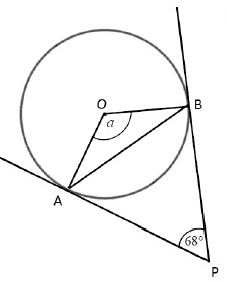
Problem 1 :

Solution :

Given, ∠APB = 68˚

∠APB + ∠PBO + ∠AOB + ∠PAO = 360˚

(angle sum property of quadrilateral)

∠AOB = 360˚ - (68˚ + 90˚ + 90˚)

∠AOB = 360˚ - 248

∠AOB = 112˚

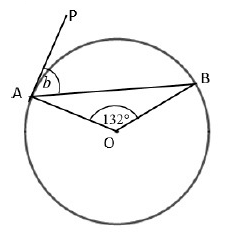
Problem 2 :

Solution :

∠OAP = 90˚

∠OAB + ∠BAP = 90˚ ---> (1)

In triangle OAB,

∠OBA + ∠OAB + ∠AOB = 180˚

Let ∠OBA = x

Since OA = OB, ∠OBA  = ∠OBA 

x + 132˚ + x = 180˚

2x + 132˚ = 180˚

2x = 180˚ - 132˚

2x = 48

x = 48/2

x = 24

By applying x = 24 in (1), we get

24 + ∠BAP = 90˚

∠BAP = 90 - 24

b = ∠BAP = 66˚

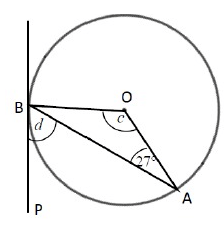
Problem 3 :

Solution :

∠OAB = 27˚, ∠OBA = 27˚

Finding c :

∠OAB + ∠OBA + ∠AOB = 180˚

27 + 27 + c = 180˚

154 + c = 180

c = 180 - 154

c = 126˚

Finding d :

∠OBA + ∠ABP = 90

27 + d = 90

d = 90 - 27

d = 63

Problem 4 :

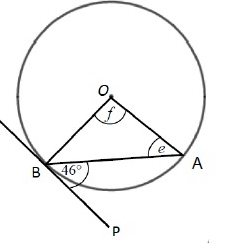
Solution :

∠OBP = 90˚

∠OBA + ∠ABP = 90˚

e + 46 = 90

e = 90 - 46

e = 44˚

∠OBA  = ∠OAB = 44˚

∠OBA + ∠OAB + ∠AOB = 180˚

44 + 44 + f = 180˚

88 + f = 180

f = 180 - 88

f = 92˚

Problem 5 :

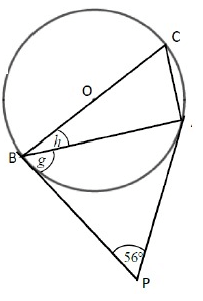
Solution :

∠PBA  = ∠PAB = g

∠BPA + ∠PBA + ∠PAB = 180˚

56 + g + g = 180

2g = 180 - 56

2g = 124

g = 62˚

Since OB is the line drawn from center of the circle to the point of contact of the tangent

g + h = 90

62 + h = 90

h = 90 - 62

h = 28˚