SMO JUNIOR SECTION 2015 SOLUTIONS PART2

Problem 6 :

Find the minimum value of the function

2015  -  [10/(x² -4x + 5)]

(A) 2000   (B) 2005    (c) 2010   

(D) 2013    (E) None of these

Solution :

In any quadratic function which is in the form

y = a(x - h)² + k

If a < 0, the function will have maximum at x = h and maximum value is k.

If a > 0, the function will have minimum at x = h and minimum is k.

x² -4x + 5 ==> x² - 2x(2) + 2² - 2² + 5

= (x - 2)² - 4 + 5

= (x - 2)² + 1

The curve x² -4x + 5 achieves the minimum at x = 2 and minimum value is 1.

So, minimum value of the given function at x = 2.

= 2015  -  [10/(2² -4(2) + 5)]

= 2015  -  (10/1)

= 2005

Problem 7 :

It is known that 99900009 is the product of four consecutive odd of squares of these four odd numbers.

(A) 40000  (B) 40010   (c) 40020

(D) 40030    (E) 40040

Solution :

Let four consecutive off numbers be

x - 3, x - 1, x + 1 and x + 3

Product of four consecutive odd numbers  = 99900009

(x - 3) (x - 1) (x + 1) (x + 3) = 99900009

(x² - 3²)(x² - 1²) = 99900009

(x² - 9)(x² - 1) = 99900009

Let x² = y

(y - 9) (y - 1) = 99900009

y² - 10y + 9 - 99900009 = 0

y² - 10y - 99900000 = 0

(y - 9990)(y - 10000) = 0

y = 9990 and y = 10000

x² = 9990 and x² = 10000

x = 100

So, the required odd numbers are 97, 99, 101, 103.

=  97² + 99² + 101² + 103²

=  9409 + 9801 + 10201 + 10609

= 40020

Problem 8 :

The lengths of the sides of the triangle are

x², 22 - x and x - 2

The total number of possible integer value of x is.

(A) 0       (B) 1      (C) 2       (D) 3    (E) 4

Solution :

Let a = x², b = 22 - x and c = x - 2

If a, b and are the sides of the triangle, then 

a + b > c, b + c > a, c + a > b 

x - 2 + x² > 22 - x

x + x - 2 - 22 + x² >0

x² + 2x - 24 > 0

(x + 6)(x - 4) > 0

x > -6 and x > 4

x² > 4² and 20 > x² 

No values of x (integer) will not satisfy this condition. So, 0 is the answer.

Problem 9 :

Find the value of 

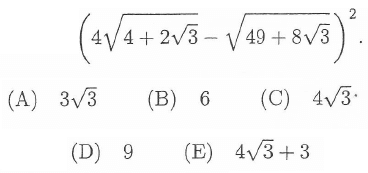
Solution :

(1) - (2)

= (4√3 + 4 - 4√3 - 1)²

= 3²

So, the answer is 9.

Problem 10 :

If x and y satisfy the equation 2x² + 3y² = 4x, the maximum value of 10x + 6y² is

(A) 2       (B) 9/2      (C) 20       (D) 81/4    (E) None

Solution :

From 2x² + 3y² = 4x

3y² = 4x - 2x²

3y² = 2x(2 - x)

range is 0 ≤ x ≤ 2

Multiplying by 2.

6y² = 8x - 4x²

10x + 6y² = 10x + 8x - 4x²

= 18x - 4x² ----(1)

To find the maximum value, converting into the form

y = a(x - h)² + k

= -4x² + 18x

Maximum at x = 2, to find maximum value

By applying x = 2 in (1), we get

= 18(2) - 4(2)²

= 36 - 16

= 20

So, the maximum value is 20.