SMO JUNIOR SECTION 2015 SOLUTIONS PART1

Problem 1 :

Among the five numbers 5/9, 4/7, 3/5, 6/11 and 13/21 which one has the smallest value ?

(A)  5/9     (B) 4/7     (C)  3/5   (D)  6/11     (E)  13/21

Solution :

5/9, 4/7, 3/5, 6/11, 13/21

LCM (9, 7, 5, 11, 21)

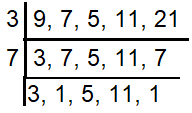
LCM = 3 x 7 x 3 x 5 x 11 ==>  3465

Problem 2 :

Adrian, Biliy, Christopher, David and Eric are the five starters of a school's basketball team. Two among the five shoot with their left hand while the rest shoot with their right hand. Among the five, only two are more than 1.8 meters in height. Adrian and Billy shoot with the same hand, but Christopher and David shoot with different hands. Biliy and Christopher are respectively the shortest and tallest member of the team, while Adrian and David have the same height. Who is more than 1.8 meters tall and shoots with his left hand? 

(a)  None (B) Only Christopher (C) Only Eric

Christopher and Eric (E) Not enough information to ascertain

Solution :

Not enough information

Problem 3 :

How many ways are there to arrange 3 identical blue balls and 2 identical red balls in a row if the two red balls must always be next to each other?

(A) 2   (B) 4    (c) 5    (D) 10    (E) 20

Solution :

Number of red balls = 2

Number of blue balls = 3

Since 2 red identical balls should be next to each other, take it as one unit.

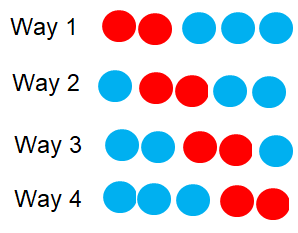
There are 4 ways.

Problem 4 :

If. a,b and c are positive real numbers such that

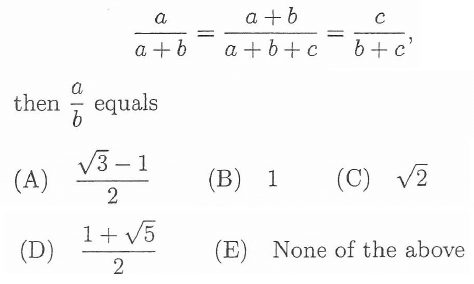
By applying a = c in ac = ab + b²

a² = ab + b²

a² - ab - b² = 0

Now we have quadratic equation in terms of a.

To solve for a, we use formula

a = 1, b = -b and c = -b²

So, option D is correct.

Problem 5 :

In the figure below, each distinct letter represents a unique digit such that the arithmetic sum holds. What is the digit represented by the letter B?

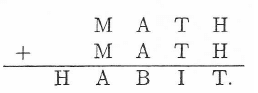
(A) 0   (B) 2    (c) 4    (D) 6    (E) 8

Solution :

Let H = 1

               M      A       2      1

               M      A       2      1

       ------------------------------------

       H      A       B      4      2

Case 1 :

If A = 3, then A + A = 6

If M = 5, then M + M = 5 + 5 => 10 (not A)

Case 2 :

If A = 4, then A + A = 8

If M = 5, then M + M = 10 (not A)

Changing M alone,

If M = 6, then M + M = 12 (not A)

Case 3 :

By changing the value of A now,

If A = 5, then A + A = 10 (in the place of B, put 0 and carry over 1)

If M = 7, then M + M = 14 + 1 => 15 (we will write 5 along and carry over 1). We get the value of A.

So, the value of B is 0.