SMO JUNIOR SECTION 2012 SOLUTIONS PART 5

Problem 14 :

Find the four digit number

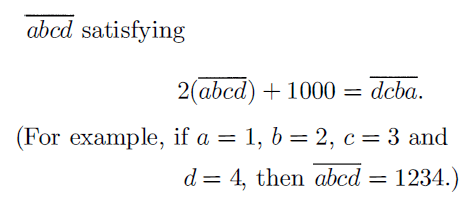
Solution :

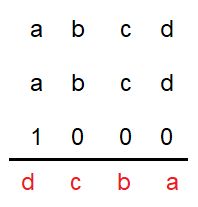
From the picture above, it is very clear

2d = a, then 2d must be even and a is also an even.

2a+1 = d,

2a+1 ≤ d ≤ 9

By applying any one of the following values of a,

a = 2 or a = 4 or a = 6, the above condition can be satisfied.

• If a = 2, then 2a + 1 ≤ d will become 5 ≤ d, 
• This will work only if d = 6

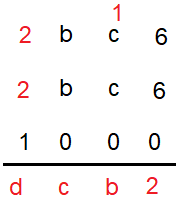
2c + 1 = b

2b = 10 + c

will not give integer solution.

2c + 1 = 10 + b

If c = 9 and b = 9

19 = 19

 a = 2, b = c = 9 and d = 6

So, the required number is 2996.

Problem 15 :

Suppose x and y are real number satisfying 

x² + y² - 22x - 20y + 221 = 0. Find xy.

Solution :

x² + y² - 22x - 20y + 221 = 0

x² - 22x + y²- 20y + 221 = 0

x² - 2 ⋅ x ⋅ 11 + 11² - 11²  + y²- 2 ⋅ y ⋅ 10 + 10² - 10² + 221 = 0

(x - 11)² - 11² + (y - 10)² - 10² + 221 = 0

(x - 11)² + (y - 10)² - 121 - 100 + 221 = 0

(x - 11)² + (y - 10)² = 0

Will become 0, only when x = 11 and y = 10

So, the value of xy = 110.

Problem 16 :

Let m and n be positive integers satisfying 

mn² + 876 = 4mn + 217 n

Find the sum of all possible values of m.

Solution :

mn² + 876 = 4mn + 217 n

It is enough to find the value of m, so recreate the equation as n = 

mn² - 217n = 4mn - 876

n(mn - 217) = 4mn - 876

n = (4mn - 876) / (mn - 217)

n = 4 - [8 / (mn - 217)]

Here mn - 217 = ±1, ±2, ±4, ±8

Since m is integer,

m = 216/12 ==> 18

m = 215/3 ==>  75

Sum of values of m = 75 + 18 ==> 93

Problem 17 :

For any real number x, let ⌊x⌋ denote the largest integer less than or equal to x. Find the value of ⌊x⌋ of the smallest x satisfying ⌊x²⌋ - ⌊x⌋² = 100.

Solution :

x = ⌊x⌋ + {x}

100 ≤  (⌊x⌋ + {x}⁾² -  ⌊x⌋²

100 ≤  ⌊x⌋² + 2⌊x⌋{x} + {x}² -  ⌊x⌋²

100 ≤  2⌊x⌋{x} + {x}²

100 ≤  2⌊x⌋ + 1

S o  x ≥ 50 and x² ≥ ⌊x²⌋ = 100 + 50² = √2600. On the other and, x = √2600 is a solution.