SMO JUNIOR SECTION 2012 SOLUTIONS PART 4

Problem 11 :

Let a and b be real numbers such that a > b, 2^a + 2^b = 75 and 2^-a + 2^-b = 12^-1. Find the value of 2^a-b

Solution :

2^a + 2^b = 75   ---(1)

2^-a + 2^-b = 12^-1   ---(2)

(1) x (2)

(2^a + 2^b)(2^-a + 2^-b) = 75 x (1/12)

2^a-a + 2^a-b + 2^b-a + 2^b-b = 75/12

1 + 2^a-b + 2^b-a + 1 = 75/12

2 + 2^a-b + 2^-(a-b) = 75/12

2^a-b + 2^-(a-b) = (75/12) - 2

2^a-b + 2^-(a-b) = (51/12)

2^a-b + 2^-(a-b) = (17/4)

2^a-b + 2^-(a-b) = 4 + (1/4)

Then, 2^a-b = 4

Problem 12 :

Find the sum of all positive integers x such that 

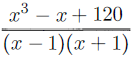
is an integer.

Solution :

The given fraction is an improper fraction. Converting it into mixed fraction, we get

To get integer, it is necessary to be x² - 1 also be integer.

Factors of 120 are

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120

The possible values of x² - 1 are

0, 2, 3, 4, 5, 11

Sum of (0, 2, 3, 4, 5, 11) :

= 0 + 2 + 3 + 4 + 5 + 11

= 25

Problem 13 :

Consider the equation

√(3x²-8x+1) + √(9x²-24x-8) = 3

It is known that the largest root of the equation is - k times the smallest root . Find k.

Solution :

√(3x²-8x+1) + √(9x²-24x-8) = 3

y = 2 and y = -5 (rejected because y should be greater than or equal to 0.)

since k = 2

3x² - 8x + 1 = 2²

3x² - 8x + 1 = 4

3x² - 8x - 3 = 0

(x - 3)(3x + 1) = 0

x = 3 and x = -1/3 ==> -3^-1

The largest root = 3, which is equal to -k x  the smallest root.

3 = -k(-1/3)

3 = k/3

k = 9

So, the answer is 9.