SMO 2013 JUNIOR SECTION

Problem 10 :

Let S be the smallest positive multiple of 15, that comprises exactly 3k digits with k 0's, k 3's and k 8's. Find the remainder when S is divided by 11.

(a)  0    (b)  3    (c)  5     (d)  6    (e)  8

Solution :

Since S is the multiple of 15, it should be multiple of 3 as well 5.

• If it is multiple of 3, its sum of the digits should be divisible by 3.
• If it is multiple of 5, its unit digit should be 0 or 5.

Possible values to fill up in the places are 0, 3, and 8. Accordingly the condition, the unit digit can be fixed with 0.

The required number will consist of 9 digits(since it is the smallest number).

3 ==> 0's, 3 ==> 3's and 3 ==> 8's

300338880

Sum of the digits = 3 + 0 + 0 + 3 + 3 + 8 + 8 + 8 + 0

= 9 + 24 ==>  33(divisible by 3)

Divisibility rule for 11 :

Find the difference of sum of alternative digits.

3 + 0 + 3 + 8 + 0 ==>  14

0 + 3 + 8 + 8 ==> 19

14 - 19 ==> 5 (mod 11) ==> 6

So, the required remainder is 6.

Problem 12 :

If the graphs of y = x² + 2ax + 6b and y = x² + 2bx + 6a intersect at only one point in the xy-plane, what is the x-coordinate of the intersection ?

Solution :

To find the point of intersection, we can solve the system of equations.

y = x² + 2ax + 6b ---(1)

y = x² + 2bx + 6a ----(2)

(1) = (2)

x² + 2ax + 6b = x² + 2bx + 6a

2ax + 6b = 2bx + 6a

2ax - 2bx + 6b - 6a = 0

2x(a - b) + 6(b - a) = 0

2x(a - b) - 6(a - b) = 0

Dividing by (a - b) on both sides.

2x - 6 = 0

2x = 6

x = 6/2

x = 3

So, the required x-coordinate is 3.

Problem 17 :

Let ABCD be a square and X and Y be the points such that lengths of XY, AX and AY are 6, 8 and 10 respectively. The area of ABCD can be expressed as m/n units where m and n are positive integers without common factors. Find the value of m + n.

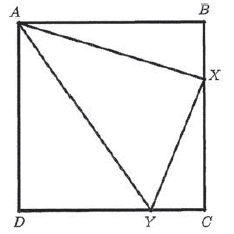
Solution :

AY = 10, XY = 6 and AX = 8

(AY)² = (XY)² + (AX)²

10² = 6² + 8²

Since it satisfies Pythagorean theorem, AXY must be a right triangle.

Area of square = AB² = BC² = CD² = DA²

In triangles ABX and CXY.

∠ABX = ∠XCY

∠AXB = ∠XYC

AX/XY = AB/XC

8/6 = AB/XC

4/3 = AB/XC

4/3 = AB/(BC - BX)

4/3 = AB/(AB - BX)

4(AB - BX) = 3AB

4AB - 4BX = 3AB

AB = 4BX  ---(1)

Area of square = (AB)² = (4BX)²

(AX)² = (AB)² + (BX)²

8² = (4BX)² + (BX)²

64 = 16(BX)² + (BX)²

17 (BX)² = 64

BX = 8/√17 

By applying the value of BX in (1), we get

AB = 4(8/√17)

AB = (32/√17)

(AB)² = (32/√17)² ==> 1024 / 17

m + n = 1024 + 17 ==> 1041

Problem 20 :

Let a, b and c be real numbers such that 

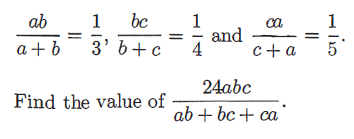
Solution :

Problem 27 :

Find the least positive integer n such that

2⁸ + 2¹¹ + 2ⁿ

is a perfect square.

Solution :

Since 2⁸ + 2¹¹ + 2ⁿ is a perfect square.

Let the required perfect square be m².

2⁸ + 2¹¹ + 2ⁿ = m²

2ⁿ = m² - 2⁸ - 2¹¹

2ⁿ = m² - 2⁸ (1 + 2³)

2ⁿ = m² - 2⁸ (9)

2ⁿ = m² - 2⁸ (3²)

2ⁿ = m² - (3(2⁴))²

2ⁿ = m² - (48)²

2ⁿ = (m + 48)(m - 48)

If 2^k = m + 48 ---(1), then 2^n-k = m - 48 ----(2)

(1) - (2)

2^k - 2^n-k  = 96

Decomposing 96, we get2⁵ x 3

2^n-k(2^2k-n - 1) = 2⁵ x 3

n - k = 5 and 2k - n = 2

Adding these two

k = 7

Applying the value of k, we get

n - 7 = 5

n = 12

So, the answer is 12.

Problem 34 :

What is the smallest positive integer value of n such that the following statements is always true ?

In any group of 2n - 10 persons,  there are always at least 10 persons who have the same birthdays.

(For this question, you may assume that are exactly 365 different possible birthdays)

Solution :

We can say as, if n + 1 objects are put into n boxes, then at least one box contains two or more objects.

In any group of 365 x 9 + 1 persons, there must be at least persons who share the same birthdays.

So, in the group of 3286 persons at least 10 will share the same birthdays.

Here, 2n - 10 ≥ 3286

2n ≥ 3296

n ≥ 1648

So, the smallest value of n is 1648.

Applying n = 1647

2(1647) - 10 = 3284 < 365 x 9

and it is possible for each of the 365 different birthdays to be shared by at most 9 persons.

Problem 35 :

What is the smallest positive integer n, where n ≠ 11, such that the highest common factor of n - 11 and 3n + 20 is greater that 1 ?

Solution :