SAT TRIGONOMETRY PRACTICE PROBLEMS

Problem 1 :

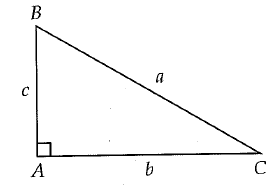
Given right triangle ABC above which of the following is equal to c/b?

A)  tan B     B)  1/tan B    C)  cos B    D)  1/cos B

Solution :

If θ is in angle B.

AC = Opposite side, AB = adjacent side, BC = hypotenuse

AB/AC = Adjacent side / Opposite side

This is reciprocal of tan B.

So, the answer 1/tan B.

Problem 2 :

sin x = cos y

In the equation above, x and y are measured in radians. Which of the following could be x in terms of y ?

A)  π/2 - y      B)  π/2 + y     C)  y - π/2     D)  π - y

Solution :

sin x = cos y

sin x = sin (π/2 - y)

x = π/2 - y

Problem 3 :

What is the value of sin 30° - cos 60° ?

Solution :

sin 30° - cos 60°

Problem 4 :

Given right triangle ABC below, which of the following gives the length of AB in terms of θ ?

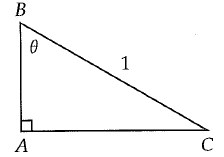
A)  sin θ     B) cos θ     C)  tan θ     D) 1/sin θ

Solution :

BC = hypotenuse, AC = opposite side and AB = adjacent side.

cos θ = adjacent side / hypotenuse

cos θ = AB/BC

cos θ = AB/1

AB = cos θ

Problem 5 :

In the xy plane below, a circle with radius 5 has its center at the origin. Point A lies on the circle and has coordinates (m, n). What is n in terms of θ ?

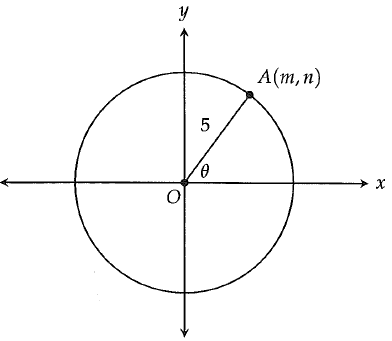
A)  5 sin θ     B) 5 cos θ     C)  tan θ     D) 5(sin θ + cos θ)

Solution :

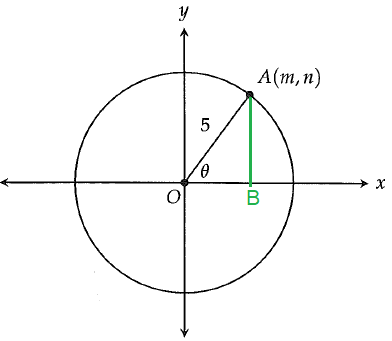
m = OB = adjacent side, n = AB = opposite side

OA = hypotenuse

tan θ = opposite side/hypotenuse

tan θ = AB/OA

tan θ = AB/5

AB = 5 tan θ

Problem 6 :

Given the right triangle below, which of the following is equal to a ?

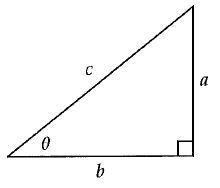
A)  a tan θ    B)  b sin θ       C) c sin θ    D) c cos θ

Solution :

a = opposite side, c = hypotenuse and b = adjacent side

sin θ = Opposite side  / hypotenuse

sin θ = a/c

a = c sin θ

Problem 7 :

In the figure given below ∠BAC = 30°,  ∠BCA = 45°, and AB = 8. What is the length of BC ?

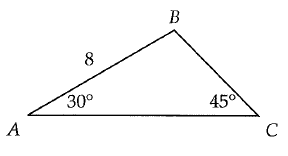
A)  4       B)  4√2     C)  4√3    D) 8√2

Solution :

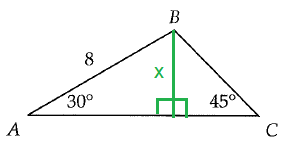
Let x be the smaller side.

2(smaller side) = hypotenuse

2x = 8

x = 4

BC is the hypotenuse for the triangle that we have in right side.

BC = √2 (smaller side)

BC = 4√2

Problem 8 :

sin 24 = cos 3k + 6

In the equation above, the angle measures are in degrees. If 0° < k < 90°, what is the value of k ?

Solution :

sin 24 = cos (3k + 6) -----(1)

sin θ = cos (90 - θ)

sin 24 = cos (90 - 24)

sin 24 = cos 66

Applying the value of sin 24 in (1), we get

cos 66 = cos (3k + 6)

66 = 3k + 6

66 - 6 = 3k

3k = 60

k = 20

Problem 9 :

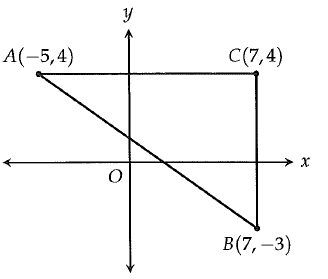
Right triangle ABC is shown in the xy-plane above. What is the value of tan A?

A)  7/12    B)  3/4    C)  7/9    D)  12/7

Solution :

tan A = Opposite side / adjacent side

BC = opposite side and AC = adjacent side.

tan A = 7/12