SAT PROBLEMS ON PERCENTAGE CHANGE

Problem 1 :

The original price of the suit is $1000. A sales man decides to discount it by 30%. Later on the manager decides to give a 15% discount off the salesman's price. What is the final price of the suit ?

a)  350      b)  485     c) 550      d)  595

Solution :

Original price of the suit = $1000

Discount = 30% of the original price

Which means, we dont have to pay 100% of the money and it is enough to pay (100 - 30)%, which is 70% of the original amount.

= 70% of 1000

= 0.70(1000)

= 700

Amount after manager's offer = (100 - 15)% of 700

= 85% of 700

= 0.85(700)

= 595

So, the final price of the suit is $595.

Problem 2 :

A large group of friends go out to dinner at a restaurant which charges them a service fee 12 percent of the original price of the meal. After this fee is factored in, the group uses the coupon to get 25% off the total. In the end, what percent discount did the group receive off the original price ?

a)  13%    b)  16%    c)  18%    d)  20%

Solution :

Let x be the original price of the meal.

112% of x = amount paid after service fee

After using 25% of coupon, amount to be paid

= 75% of 112% of x

= 0.75 (1.12x)

= 0.84x

= 84% of x

After the discount = 100 - 84

= 16

So, the group will receive 16% discount. 

Problem 3 :

The difference between two numbers is 30. One of the numbers x is 20% less than the other number, find the value of x? 

Solution :

Let x and y be the two numbers.  

One number x = 80% of y

y - x = 30

y - 0.80y = 30

0.20y = 30

y = 30/0.20

y = 150

x = 0.80y

x = 0.80(150)

x = 120

So, the required number is 120.

Problem 4 :

There are 50 tennis balls, 20 of which are blue in a container. After x blue tennis balls are removed, 25% of the tennis balls in the container are blue. What is the value of x ?

Solution :

Total number of balls = 50

Number of clue balls = 20

After removing x blue balls,

number of balls in total = 50 - x

number of blue balls = 20 - x

(20 - x) / (50 - x) = 25/100

(20 - x) / (50 - x) = 1/4

4(20 - x) = 1(50 - x)

80 - 4x = 50 - x

80 - 50 = -x + 4x

30 = 3x 

x = 10

So, the value of x is 10.

Problem 5 :

During one season, a baseball player managed to hit 25% of the balls pitched at him. Of the balls he hit, 5 percent were home runs. Which of the following expresses the estimated number of home runs this player would hit if n balls were pitched at him ?

a)  (0.25+0.05)n    b)   (0.25) (0.05)n

c)  n/(0.25)(0.5)     d)  (1.25)(1.05n)

Solution :

Number of balls pitched at him = n

25% of n = the number of balls managed to hit

Number of home runs = 5% of (25% of n)

= 0.05 (0.25n)

So, option b is correct.

Problem 6 :

Gillian scored an 84 on her midterm and a 94 on her final. which of the following best approximates the percent increase in her score from her midterm to her final ?

a)  10.6%     b)  11.9%     c)  12.1%     d)  15.5% 

Solution :

Old score = 84

New score = 94

Since the new score is greater than the old score, percentage increase happened.

Percentage increase

= { (New value - old value) / old value } x 100%

= {(94 - 84) / 94} x 100%

= (10/94) x 100%

= 0.106 x 100%

= 10.6%

So, option a is correct.

Problem 7 :

A wine manufacturer produced x bottles of wine in its first production run. In its second run, it produced 35% less. If the manufacturer produced 3900 bottles in its second run, what is the value of x ?

a)  5265     b)  5750    c)  5830    d)  6000

Solution :

Number of bottles produced in the second run = 3900

Number of bottles produced in the first run = x

Number of bottles produced in the second run = 65% of x

3900 = 0.65 x

x = 3900 / 0.65

x = 6000

Number of bottles produced in the first run = 6000.

Problem 8 :

At the start of the semester, Andrew could swim a mile in 16 minutes. At the end of the semester he could swim a mile in 12 minutes. What is the percent decrease (to the nearest percent) in his time from the start to the end of the semester ?

a)  20%     b)  25%    c)  33%    d)  40%

Solution :

Number of minutes taking last time = 16

Number of minutes he is taking at the end of the semester = 12 

Percentage decrease happened.

Percentage decrease = {(16 - 12) / 16 } x 100%

= (4/16) x 100%

= (1/4) x 100%

= 25% 

So, option b is the answer.

Problem 9 :

The table below shows the number of vowels and consonants in 4 different languages.

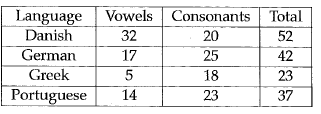
Based on the table, vowels make up approximately 38% of the alphabet in which language ?

a)  Danish    b)  German     c) Greek    d)  Portuguese

Solution :

Percentage of vowels in Danish = (32/52) x 100%

= 0.6153 x 100%

= 61.5%

Percentage of vowels in German = (17/42) x 100%

= 0.4047 x 100%

= 40.4%

Percentage of vowels in Greek = (5/23) x 100%

= 0.2173 x 100%

= 21.7%

Percentage of vowels in Portuguese = (14/37) x 100%

= 0.3783 x 100%

= 37.8%

Approximately 38%.

So, answer is option d.

Problem 10 :

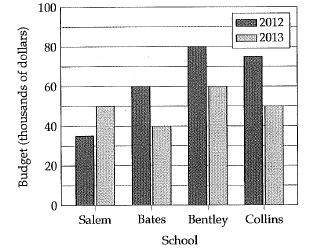
From 2012 to 2013, the total budget for all four schools decreased by approximately what percent ?

Solution :

By observing the bar graph,

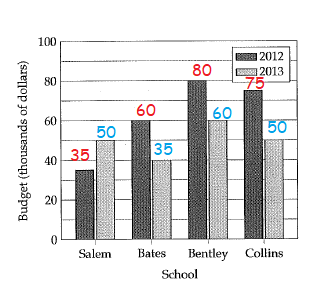
In 2012 = 35 + 60 + 80 + 75

= 250

In 2013 = 50 + 35 + 60 + 50

= 195

Percentage of decrease = { (250 - 195) / 250 } x 100%

= (55 / 250) x 100%

= 0.22 x 100%

= 22%

So, the percentage decrease is 22%.