SAT PRACTICE ON GEOMETERY WORKSHEET

Problem 1 :

What is the radius of a circle that has a circumference of π?

A) 1/4      B) 1/2     C) 1     D) 2     E) 4

Solution

Problem 2 :

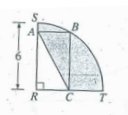
In the figure above, arc SBT is one quarter of a circle with center R and radius 6. If the length plus the width of rectangle ABCR is 8, then the perimeter of the shaded region is

A) 8 + 3π        B) 10 + 3π      C) 14 + 3π     D) 1 + 6π

E) 12 + 6π

Solution

Problem 3 :

In the xy-coordinate plane, what is the area of the square with opposite vertices at (-2, -2) and (2, 2) ?

A) 4    B) 8    C) 16     D) 32   E) 64

Solution

Problem 4 :

In rectangle ABCD, point E is the midpoint of BC. If the area of quadrilateral ABED is 2/3, what is the area of rectangle ABCD?

A)  1/2      B)  3/4      C)  8/9     D)  1       E)  8/3

Solution

Problem 5 :

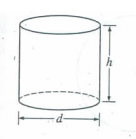
In right circular cylinder above has diameter d and height h. Of the following expressions, which represents the volume of the smallest rectangular box that completely contains the cylinder?

A) dh      B) d²h       C) dh²      D) d²h²       E) (d + h)²

Solution

Problem 6 :

If the volume of a cube is 8, what is the shortest distance from the center of the cube to the base of the cube?

A) 1     B) 2    C) 4    D) √2    E) 2√2

Solution

Problem 7 :

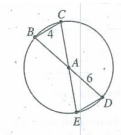
In the figure above, point A is the center of the circle and segments BD and CE are diameters. Which of the following statements is true?

A) CA > 6    B) ED > 4    C) BA  < 4   D) CA = 4   E) ED = 4

Solution

Problem 8 :

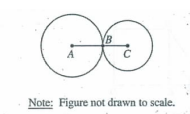
In the figure above, the two circles are tangent at point B and AC = 6. If the circumference of the circle with center A is twice the circumference of the circle with center C, what is the length of BC?

A) 1    B) 2    C) 3     D) 4    E) 6

Solution

Problem 9 :

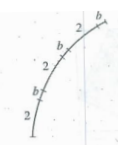
The figure above shows part of a circle whose circumference is 45. If arcs of length 2 and length b continue to alternate around the entire circle so that there are 18 arcs of each length, what is the degree measure of each of the arcs of length b ?

A) 4°    B) 6°    C) 10°    D) 16°    E) 20°

Solution

Problem 10 :

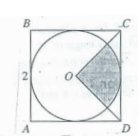
In the figure above, the circle with center O is inscribed in square ABCD. What is the area of the shaded portion of the circle?

Solution