SAT MATH PROBLEMS SYSTEM OF EQUATIONS BY ELIMINATION

Problem 1 :

3x + 4y = -23

2y - x = -19

What is the solution (x, y) to the system of equations above ?

A)  (-5, -2)       B)  (3, -8)       C)  (4, -6)     D)   (9, -6)

Solution :

     3x + 4y = -23 --- (1)

2y - x = -19

-x + 2y = -19 --- (2)

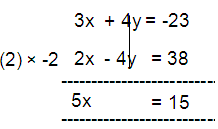
5x = 15

x = 15/5

x = 3

x = 3 substitute the equation (2).

-3 + 2y = -19

2y = -19 + 3

2y = -16

y = -16/2

y = -8

Hence, (3, -8) is required solution.

So, option B) is correct.

Problem 2 :

x + y = 0

3x - 2y = 10

Which of the following ordered pairs (x, y) satisfies the system of equations above ?

A)  (3, -2)  B)  (2, -2)   C)   (-2, 2)   D)   (-2, -2)

Solution :

x + y = 0 --- (1)

3x - 2y = 10 --- (2)

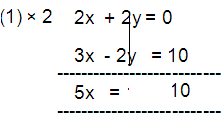
5x = 10

x= 10/5

x = 2

x = 2 substitute the equation (1).

2 + y = 0

y = -2

So, the value of x and y is (2, -2).

Hence option B) is correct.

Problem 3 :

ax + by = 12

2x + 8y = 60

In the system of equations above, a and b are constants. If the system has infinitely many solutions, what is the value of a/b ?

Solution :

ax + by = 12 --- (1)

2x + 8y = 60 --- (2)

Equation (1) multiplied by 5.

Problem 4 :

y = 3

y = ax² + b

In the system of equations above, a and b are constants. For which of the following values of  a and b does the system of equations have exactly two real solutions ?

A)  a = -2, b = 2        B) a = -2, b = 4 

C)  a = 2, b = 4          D)  a = 4, b = 3

Solution :

y = 3

y = ax² + b

Consider option A)

3 = -2x² + 2

-2x² + 2 - 3 = 0

-2x² - 1 = 0

-2x² = 1

x² = -1/2

x = √-1/2

Option A) is not correct.

Consider option B)

3 = -2x² + 4

-2x² + 4 - 3 = 0

-2x² + 1 = 0

-2x² = -1

x² = -1/-2

x = √1/2

So, the value of a = -2, b = 4. 

Hence option B) is correct.

Problem 5 :

x + y = -9

x + 2y = -25

According to the system of equations above, what is the value of x ?

Solution :

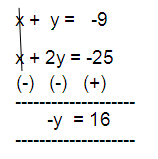
y = -16

So, the value of y is -16.

Problem 6 :

x + y = 29

x + 2y = 12

If the ordered pair (x, y) is the solution to the system of equations above, what is the value of y ?

A)  -17      B)  12      C)  46      D)  75

Solution :

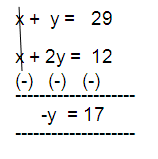
y = -17

So, option A) is correct.

Problem 7 :

4x - 2y + 3 = 8

3x + 6y = 8y - x + 5

How many solutions does the system of equations shown above have ?

A)  0      B)  1       C)   2      D) Infinitely many

Solution :

4x - 2y = 8 - 3

4x - 2y = 5 --- (1)

3x + 6y = 8y - x + 5

3x + 6y - 8y + x = 5

4x - 2y = 5 --- (2)

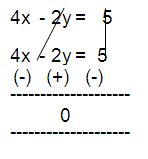
This equations has infinitely many solutions.

So, option D) is correct.

Problem 8 :

If

5b = 6a + 16 and 9a = 7b - 20

then what is the value of 3a - 2b ?

A)   -8      B)   -4       C)   4      D)  8

Solution :

Given, 5b = 6a + 16

9a = 7b - 20

3a - 2b = -4

So, option B) is correct.

Problem 9 :

If the ordered pair (x, y) satisfies the system of equations above, what is the value of y ?

A)  0      B)  7      C)  10      D)  11

Solution :

So, the value of y is 11.

So, option D) is correct.

Problem 10 :

2x - 3y = -3

-12 = -4x + y

In what quadrant will the lines represented by the equations above intersect ?

A) Quadrant I   B)  Quadrant II  C) Quadrant III 

D)  Quadrant IV

Solution :

2x - 3y = -3 --- (1)

-12 = -4x + y --- (2)

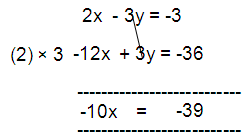
x = 39/10

x = 39/10 substitute the equation (1).

2(39/10) - 3y = -3

39/5 - 3y = -3

39/5 + 3 = 3y

(39 + 15)/5 = 3y

54/5 = 3y

y = 1/3 × 54/5

y = 54/15

The lines intersect in I Quadrant.

So, option A) is correct.