SAT MATH PRACTICE QUESTIONS IN QUADRATIC EQUATION

Problem 1 :

In the xy plane, what is the distance between the two x-intercepts of the parabola 

y = x² - 3x - 10

(a)  3      (b)  5    (c)  7    (d)  10

Solution

Problem 2 :

What are the solutions to x² + 4x + 2 = 0 ?

(a)  -2 ± √2      (b)  2 ± √2   (c) -2 ± 2√2    (d)  -4 ± 2√2

Solution

Problem 3 :

If a < 1 and 2a² - 7a + 3 = 0, what is the value of a ?

Solution

Problem 4 :

3x² + 10x = 8

If a and b are two solutions to the equation above and a > b, what is the value of b² ?

Solution

Problem 5 :

What is the sum of solutions of (2x - 3)² = 4x + 5 ?

Solution

Problem 6 :

y = -3 and y = x² + cx

In the system of equations above, c is a constant. For which of the following values of c does the system of equations have exactly two real solutions ?

(a)  -4   (b)  1    (c)  2     (d)  3

Solution

Problem 7 :

At which of the following points does the line with equation

y = 4

intersect the parabola

y = (x + 2)² - 5

in the xy - plane ?

(a)  (-1, 4) and (-5, 4)      (b)  (1, 4) and (-5, 4)

    (c)  (1, 4) and (5, 4)    (d)  (-11, 4) and (7, 4)

Solution

Problem 8 :

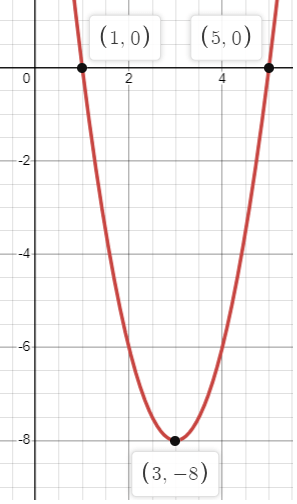
Which of the following equations represents the parabola shown in the xy-plane above ?

(a) y = (x - 3)² - 8        (b)  y = (x + 3)² + 8

(c)  y = 2(x - 3)² - 8     (d)  y = 2(x + 3)² - 8

Solution

Problem 9 :

For what value of t does the equation v = 5t - t², result in the maximum value of v ?

Solution

Problem 10 :

P = m² - 100 m - 120000

The monthly profit of a mattress company can be modeled by the equation above, where P is the profit in dollars, and m is the number of mattresses sold. What is the minimum number of mattresses the company must sell in a given month so that it does not lose money during that month ?

Solution

Problem 11 :

y = -3

y = ax² + 4x - 4

In the system of equations above, a is constant. For which of the following values of a does the system of equations have exactly one real solution ?

(a)  -4   (b)  1    (c)  2     (d)  4

Solution

Problem 12 :

f(x) = -x² + 6x + 20

The function f is defined above. Which of the following equivalent forms of f(x) displays the maximum value of f as a constant or coefficient ?

(a) y = -(x - 3)² + 11        (b)  y = -(x + 3)² + 29

(c)  y = -(x + 3)² + 11     (d)  y = -(x + 3)² + 29

Solution

Problem 13 :

y = a(x - .3)(x - k)

In the quadratic equation above, a and k are constants. If the graph of the equation in the xy plane is a parabola with vertex (5, -32), what is the value of a ?

Solution

Problem 14 :

In the xy plane, the line y = 2x + b intersects the parabola

y = x² + bx + 5

at the point (3, k). If b is a constant, what is the value of k ?

Solution