PSAT MATH ALGEBRA PRACTICE QUESTIONS

Problem 1 :

7m = 5(n + p)

The given equation relates the positive numbers m, n, and p. Which equation correctly gives n in terms of m and p ?

Solution

Problem 2 :

A rectangle has a length that is 15 times its width. The function y = (15 w)(w) represents this situation, where y is the area, in square feet, of the rectangle and y > 0 . Which of the following is the best interpretation of 15w in this context?

A) The length of the rectangle, in feet

B) The area of the rectangle, in square feet

C) The difference between the length and the width of the rectangle, in feet

D) The width of the rectangle, in feet

Solution

Problem 3 :

x + 2y = 6

x - 2y = 4

The solution to the given system of equations is (x, y). What is the value of x ?

A) 2.5      B) 5      C) 6      D) 10

Solution

Problem 4 :

The table shows the frequency of values in a data set

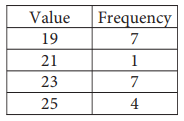
What is the minimum value of the data set?

Solution

Problem 5 :

A number x is at most 17 less than 5 times the value of y. If the value of y is 3, what is the greatest possible value of x ?

Solution

Problem 6 :

5x² - 37x - 24 = 0

What is the positive solution to the given equation?

A) 3/5    B) 3     C) 8      D) 37

Solution

Problem 7 :

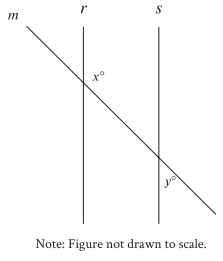
In the figure shown, lines r and s are parallel, and line m intersects both lines. If y < 65 , which of the following must be true?

A) x < 115     B) x > 115    C) x + y < 180     D) x + y > 180

Solution

Problem 8 :

In the given function f, a is a constant. The graph of function f in the xy-plane, where y = f(x) , is translated 3 units down and 4 units to the right to produce the graph of y = g(x). Which equation defines function g ?

Solution

Problem 9 :

A machine launches a softball from ground level. The softball reaches a maximum height of 51.84 meters above the ground at 1.8 seconds and hits the ground at 3.6 seconds. Which equation represents the height above ground h, in meters, of the softball t seconds after it is launched?

A) h(t) = -t² + 3.6                  B) h(t) = -t² + 51.84

C) h(t) = -16(t - 1.8)² - 3.6          D) h(t) = -16(t - 1.8)² + 51.84

Solution

Problem 10 :

In triangle ABC , the measure of angle B is 90° and BD is an altitude of the triangle. The length of AB is 15 and the length of AC is 23 greater than the length of AB. What is the value of BC/BD ?

A) 15/38     B) 15/23      C) 23/15       D) 38/15

Solution

Problem 11 :

f (x) = (x + 7)² + 4

The function f is defined by the given equation. For what value of x does f (x) reach its minimum?

Solution