AP CALCULUS QUESTONS ON DERIVATIVES

Problem 1 :

If (x + 2y) (dy/dx) = 2x - y, what is the value of d²y/dx² at the point (3, 0) ?

A)  -10/3      B)  0     C)  2    D) 10/3   E)  Undefined

Solution :

(x + 2y) (dy/dx) = 2x - y

f'(x) = dy/dx = (2x - y) / (x + 2y)

The given function is implicit function.

So, option A is correct.

Problem 2 :

For t ≥ 0, the position of a particle moving along the x-axis is given by x(t) = sin t - cos t. What is the acceleration of the particle at the point where the velocity is equal to 0 ?

A)  -√2    B)  -1      C)  0      D)  1      E) √2

Solution :

x(t) = sin t - cos t

x'(t) = cos t - (-sin t)

v(t) = cos t + sin t

v(t) = 0

cos t + sin t = 0

cos t = - sin t

sin t/cost = - 1

tan t = -1 

t = tan^-1(-1)

t = - π/4 not positive, so t = 3π/4

v(t) = cos t + sin t

v'(t) = -sin t + cos t

a(t) = -sin(3π/4) + cos (3π/4)

a(t) = -1/√2 - 1/√2

a(t) = -2/√2

a(t) = -√2(√2)/√2

a(t) = -√2

So, option A is correct.

Problem 3 :

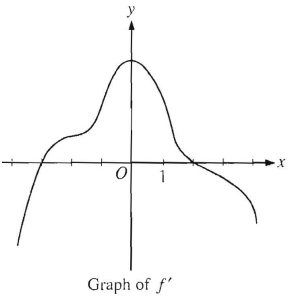
The graph f', the derivative of the function, f is shown above. Which of the following statements must be true ?

I)  f has relative minimum at x = -3

II) The graph of f has a point of inflection at x = -2

III) The graph of f is concave down for 0 < x < 4

A)  I only    B)  II only   C)  III only    D)  I and II only 

E)  I and III only

Solution :

I)  f has relative minimum at x = -3, it is true.

II) The graph of f has a point of inflection at x = -2

If x = -2 is a point of inflection, then it should be the x-intercept in derivative graph.

III) The graph of f is concave down for 0 < x < 4

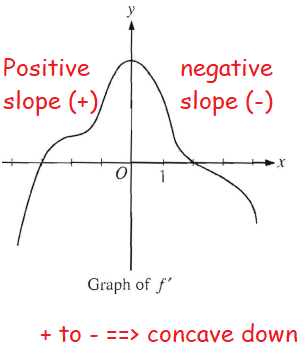
So, it is true. The true statements are I and III only (option E).

Problem 4 :

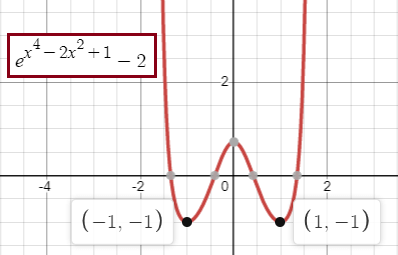
The graph of y = e^{tan x}- 2 crosses the x-axis at one point in the interval [0, 1]. What is the slope of the graph at this point ?

A)  0.606    B)  2      C) 2.242     D)  2.961    E)  3.747

Solution :

y = e^{tan x}- 2

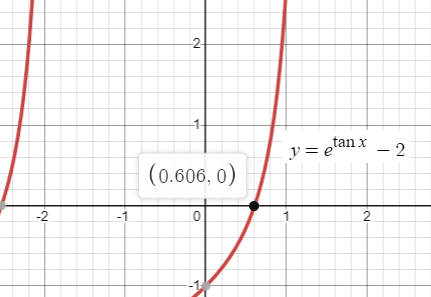
Using graphing calculator, we get the x-intercept between [0, 1] 0.606.

y = e^{tan x}- 2

y' = e^{tan x} (sec² x) - 0

y' = e^{tan x} sec² x

y'(0.606) = e^{tan (0.606)} sec² (0.606)0.010

= 1.99 (1.47)

= 2.92

So, option D is correct.

Problem 5 :

f'(x) = √(x⁴+1) + x³ - 3x, then f has a local maximum at x = ?

A)  -2.314    B)  -1.332       C)  0.350    D)  0.829     E) 1.234

Solution :

f'(x) = √(x⁴+1) + x³ - 3x

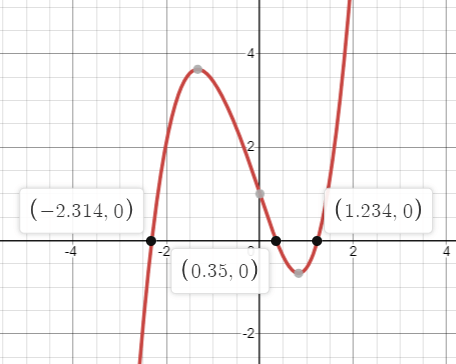
Using graphing calculator, it is clear that -2.314, 0.35 and 1.234 are x-intercepts of the first derivative. So, these must be critical numbers for the function f(x).

In between (-2.314 to 0.35), f'(x) is above x-axis, f(x) must be increasing function in this interval.

Between (0.35 to 1.234), f'(x) is below the x-axis, f(x) must be decreasing function.

Increasing ----> Decreasing

maximum will be at x = 0.35

So, option C is correct.

Problem 6 :

For -1.5 < x < 1.5, let f be a function with first derivative given by

Which of the following are all intervals on which graph of f is concave down ?

A)  (-0.418, 0.418)      B)  (-1, 1)

C)  (-1.354, -0.409) and (0.409, 1.354)

D)  (-1.5, -1) and (0, 1)

E)  (-1.5, -1.354) (-0.409, 0) and (1.354, 1.5)

Solution :

Slopes decreasing in f'(x) = concave down

Slopes increasing in f'(x) = concave up

On the intervals (-1.5, -1) and (0, 1), the slopes are decreasing. So concave down on these two values of x. Option D

Problem 7 :

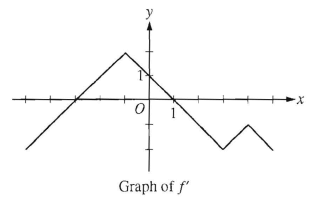
The graph of f', the derivative of f is shown above. The function f has local maximum at x = ?

A)  -3         B)  -1         C)  1         D)  3        E) 4

Solution :

f'(x) = 0, when x = -3 and x = 1

• These are critical points, to the left of -3, the graph is below the x-axis. So, it is decreasing.
• After -3 upto 1 it is above the x-axis. So, it is increasing.
• After 1, it is below the x-axis. So, it is decreasing.

Decreasing --> increasing --> decreasing

The, local maximum is at x = 1, option C

Problem 8 :

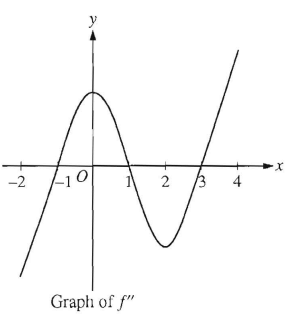
The graph of f'', the second derivative f, is shown above -2 ≤ x ≤ 4. What are all intervals on which the graph of the function f is concave down ?

A)  -1 < x < 1       B)  0 < x < 2      C) 1 < x < 3

D) -2 < x < -1       E)  -2 < x < -1 and 1 < x < 3

Solution :

In the graph of second derivative, the curve lies below x-axis can be considered as concave down.

The curve lies above x-axis can be considered as concave up.

On -2 < x < -1 and 1 < x < 3, the function f is concave down. Option E.

Problem 9 :

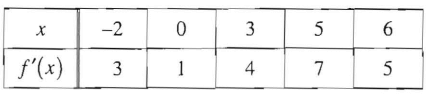
Let f be a polynomial with values of f'(x) at selected values of x given in the table above. Which of the following must be true for -2 < x < 6?

A)  The graph of f is concave up.

B)  The graph of f has at least two points of inflection

C) f is increasing

D)  f has no critical points.

E)  f has at least two relative extrema

Solution :

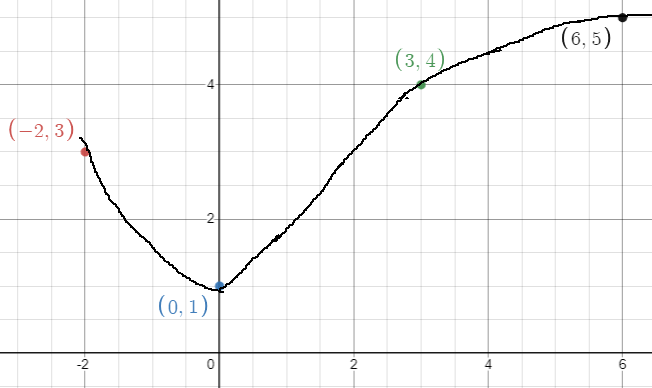
Since some selected points only is given, we cannot decide the concavity, increasing functions and critical points.

By connecting all the points given, there is two points of inflections. So, option B is is correct.

Problem 10 :

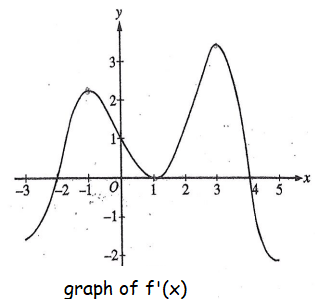
The graph of the derivative of a function f is shown in the figure above. The graph has horizontal tangent lines at x = -1, x = 1 and x = 3. At which of the following values of x does f have a relative maximum ?

A)  -2 only      B)  1 only    C)  4 only    D)  -1 and 3 only

E)  -2, 1 and 4.

Solution :

Increasing slope ---> Decreasing slope will produce relative maximum.

x-intercepts of f'(x) are critical points of f(x).

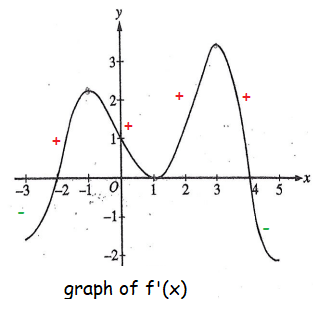
Increasing slope to decreasing slope happens only at x = 4. So, relative maximum is at x = 4.