PROBLEMS ON SURFACE AREA OF PYRAMID WITH DIFFERENT BASE

Find the surface area of the pyramid given below.

Problem 1 :

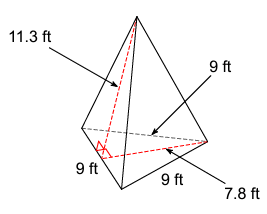
Solution :

It is triangular base pyramid.

Surface area of the given pyramid

= Sum of area of all faces including the base

Area of the base = (1/2) x base x height

Base = 9 ft, height = 7.8 ft

= (1/2) x 9 x 7.8

= 9 x 3.9

= 35.1 square ft

Area of the faces around the shape = 3 x (1/2) x 9 x 11.3

= 148.5 square ft

Surface area of the pyramid = 35.1 + 148.5

= 183.6 square ft

Problem 2 :

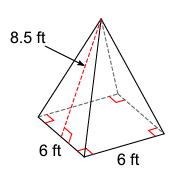
Solution :

It is square base pyramid.

Surface area of the given pyramid

= Sum of area of all faces including the base

Area of the base = a² 

= 36 square ft

Area of the faces around the shape = 4 x (1/2) x base x height 

= 2 x 6 x 8.5

= 102

Surface area of the pyramid = 36 + 102

= 138 square ft

Problem 3 :

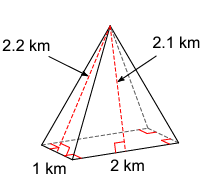
Solution :

It is rectangular base pyramid.

Surface area of the given pyramid

= Sum of area of all faces including the base

Area of the base = length x width

= 1 x 2

= 2 km²

Area of the faces around the shape

= 2 x (1/2) x 1 x 2.2 + 2 x (1/2) x 2 x 2.1

= 2.2 + 4.2

= 6.4

Surface area of the pyramid = 2 + 6.4

= 8.4 km²

Problem 4 :

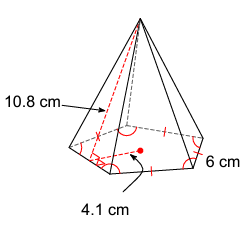
Solution :

It is pentagon base pyramid.

Surface area of the given pyramid

= Sum of area of all faces including the base

Area of the base = (1/2) x perimeter x apothem

= (1/2) x 5(6) x 4.1

= 61.5 cm²

Area of the faces around the shape

= 5 x (1/2) x 6 x 10.8

= 162 cm²

Surface area of the pyramid = 61.5 + 162

= 223.5 cm²

Problem 5 :

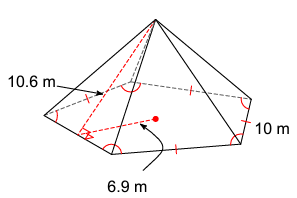
Solution :

It is pentagon base pyramid.

Surface area of the given pyramid

= Sum of area of all faces including the base

Area of the base = (1/2) x perimeter x apothem

= (1/2) x 5(10) x 6.9

= 172.5 m²

Area of the faces around the shape

= 5 x (1/2) x 10 x 10.6

= 265 m²

Surface area of the pyramid = 172.5 + 265

= 437.5 m²

Problem 6 :

A tetrahedron is a triangular pyramid whose four faces are identical equilateral triangles. The total lateral surface area is 93 square centimeters. Find the surface area of the tetrahedron.

Solution :

The total lateral surface area = 93 square cm

Base is one face and the remaining three faces will be around the shape. 

Lateral surface area = area around the shape

3(area of equilateral triangle) = 93

Area of one equilateral triangle = 93/3

= 31 square cm

Total surface area of tetrahedron = 4 (31)

= 124 cm²

Problem 7 :

You are building a bike ramp that is shaped like a square pyramid. You use two 4-foot by 8-foot sheets of plywood. How much plywood do you have left over?

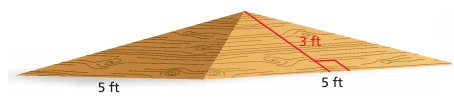
Solution :

Area of triangle =  (1/2) x base x height

Lateral surface area = 4 x (1/2) x 5 x 3

= 30 square ft

Area of one plywood sheet = 4 x 8

= 32 square ft

Left over = 32 - 30

= 2 square ft